ModernDive

Chapter 2 Data Visualization

We begin the development of your data science toolbox with data visualization. By visualizing data, we gain valuable insights that we couldn’t initially obtain from just looking at the raw data values. We’ll use the ggplot2 package as it provides an easy way to customize your plots. ggplot2 is rooted in the data visualization theory known as The Grammar of Graphics (Wilkinson 2005), developed by Leland Wilkinson.

At their most basic, graphics/plots/charts (we use these terms interchangeably in this book) provide a nice way to explore the patterns in data, such as the presence of outliers, distributions of individual variables, and relationships between groups of variables. Graphics are designed to emphasize the findings and insights you want your audience to understand. This does however require a balancing act. On the one hand, you want to highlight as many interesting findings as possible. On the other hand, you don’t want to include so much information that it overwhelms your audience.

As we will see, plots also help us to identify patterns and outliers in our data. We’ll see that a common extension of these ideas is to compare the distribution of one quantitative variable (i.e., what the spread of a variable looks like or how the variable is distributed in terms of its values) as we go across the levels of a different categorical variable.

Needed packages

Let’s load all the packages needed for this chapter (this assumes you’ve already installed them). Read Section 1.3 for information on how to install and load R packages.

2.1 The Grammar of Graphics

We begin with a discussion of a theoretical framework for data visualization known as “The Grammar of Graphics.” This framework serves as the foundation for the ggplot2 package which we’ll use extensively in this chapter. Think of how we construct sentences in English to form sentences by combining different elements, like nouns, verbs, particles, subjects, objects, etc. We can’t just combine these elements in any arbitrary order; we must do so following a set of rules known as a linguistic grammar. Similarly to a linguistic grammar, “The Grammar of Graphics” defines a set of rules for constructing statistical graphics by combining different types of layers. This grammar was created by Leland Wilkinson (Wilkinson 2005) and has been implemented in a variety of data visualization software platforms like R, but also Plotly and Tableau.

2.1.1 Components of the Grammar

In short, the grammar tells us that:

A statistical graphic is a mapping of data variables to aesthetic attributes of geometric objects.

Specifically, we can break a graphic into the following three essential components:

  1. data: the data set containing the variables of interest.
  2. geom: the geometric object in question. This refers to the type of object we can observe in a plot. For example: points, lines, and bars.
  3. aes: aesthetic attributes of the geometric object. For example, x/y position, color, shape, and size. Aesthetic attributes are mapped to variables in the data set.

You might be wondering why we wrote the terms data, geom, and aes in a computer code type font. We’ll see very shortly that we’ll specify the elements of the grammar in R using these terms. However, let’s first break down the grammar with an example.

2.1.2 Gapminder data

In February 2006, a statistician named Hans Rosling gave a TED talk titled “The best stats you’ve ever seen” where he presented global economic, health, and development data from the website gapminder.org. For example, for data on 142 countries in 2007, let’s consider only 6 countries in Table 2.1.

TABLE 2.1: Gapminder 2007 Data: First 6 of 142 countries
Country Continent Life Expectancy Population GDP per Capita
Afghanistan Asia 43.8 31889923 975
Albania Europe 76.4 3600523 5937
Algeria Africa 72.3 33333216 6223
Angola Africa 42.7 12420476 4797
Argentina Americas 75.3 40301927 12779
Australia Oceania 81.2 20434176 34435

Each row in this table corresponds to a country in 2007. For each row, we have 5 columns:

  1. Country: Name of country.
  2. Continent: Which of the five continents the country is part of. Note that “Americas” includes countries in both North and South America and that Antarctica is excluded.
  3. Life Expectancy: Life expectancy in years.
  4. Population: Number of people living in the country.
  5. GDP per Capita: Gross domestic product (in US dollars).

Now consider Figure 2.1, which plots this data for all 142 countries in the data.

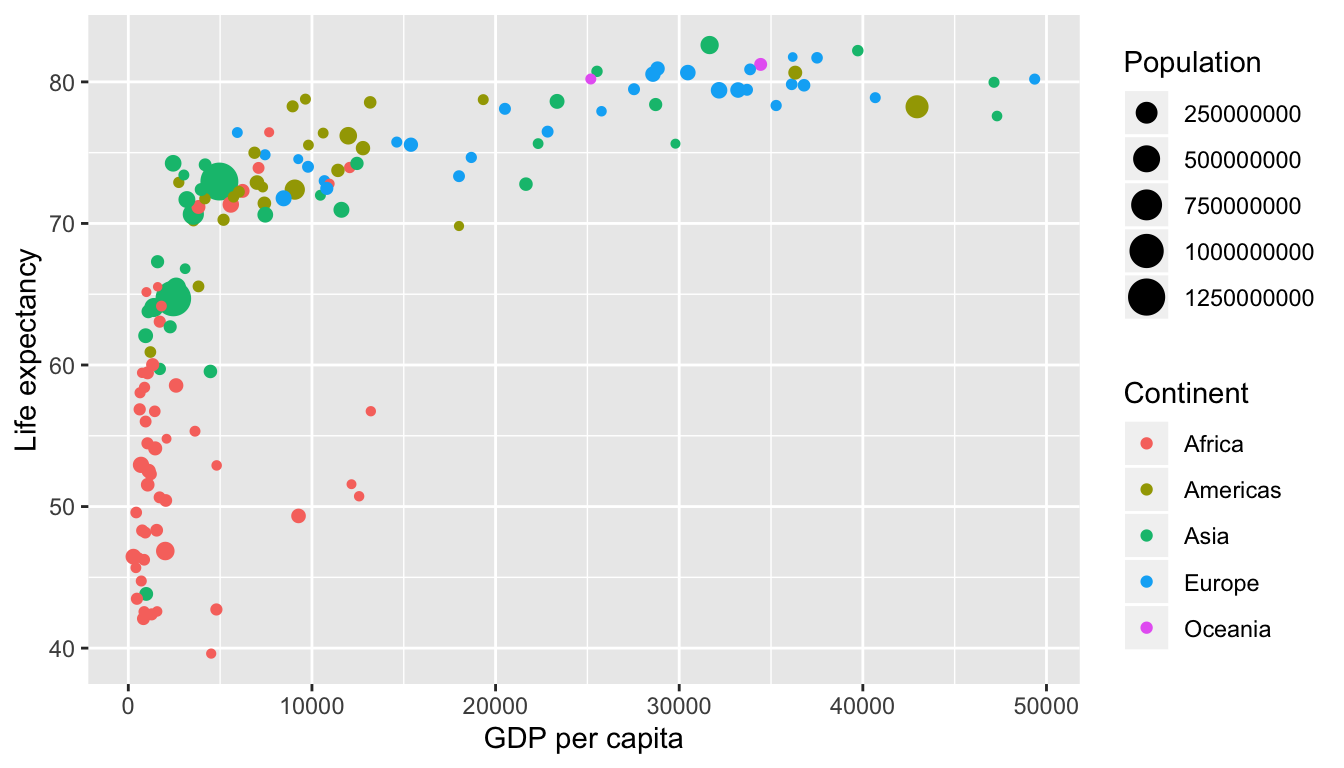
Life expectancy over GDP per capita in 2007.

FIGURE 2.1: Life expectancy over GDP per capita in 2007.

Let’s view this plot through the grammar of graphics:

  1. The data variable GDP per Capita gets mapped to the x-position aesthetic of the points.
  2. The data variable Life Expectancy gets mapped to the y-position aesthetic of the points.
  3. The data variable Population gets mapped to the size aesthetic of the points.
  4. The data variable Continent gets mapped to the color aesthetic of the points.

We’ll see shortly that data corresponds to the particular data frame where our data is saved and that “data variables” correspond to particular columns in the data frame. Furthermore, the type of geometric object considered in this plot are points. That being said, while in this example we are considering points, graphics are not limited to just points. We can also use lines, bars, and other geometric objects.

Let’s summarize the three essential components of the Grammar in Table 2.2.

TABLE 2.2: Summary of Grammar of Graphics for this plot
data variable aes geom
GDP per Capita x point
Life Expectancy y point
Population size point
Continent color point

2.1.3 Other components

There are other components of the Grammar of Graphics we can control as well. As you start to delve deeper into the Grammar of Graphics, you’ll start to encounter these topics more frequently. In this book, we’ll keep things simple and only work with these two additional components:

  • faceting breaks up a plot into several plots split by the values of another variable (Section 2.6)
  • position adjustments for barplots (Section 2.8)

Other more complex components like scales and coordinate systems are left for a more advanced text such as R for Data Science (Grolemund and Wickham 2016). Generally speaking, the Grammar of Graphics allows for a high degree of customization of plots and also a consistent framework for easily updating and modifying them.

2.1.4 ggplot2 package

In this book, we will use the ggplot2 package for data visualization, which is an implementation of the Grammar of Graphics for R (Wickham, Chang, et al. 2019). As we noted earlier, a lot of the previous section was written in a computer code type font. This is because the various components of the Grammar of Graphics are specified in the ggplot() function included in the ggplot2 package. The ggplot() function expects the following arguments (i.e. inputs) at a minimum:

  • The data frame where the variables exist: the data argument.
  • The mapping of the variables to aesthetic attributes: the mapping argument which specifies the aesthetic attributes involved.

After we’ve specified these components, we then add layers to the plot using the + sign. The most essential layer to add to a plot is the layer that specifies which type of geometric object we want the plot to involve: points, lines, bars, and others. Other layers we can add to a plot include the plot title, axes labels, visual themes for the plots, and facets (which we’ll see in Section 2.6).

Let’s now put the theory of the Grammar of Graphics into practice.

2.2 Five Named Graphs - The 5NG

In order to keep things simple in this book, we will only focus on five different types of graphics in this book, each with a commonly given name. We term these “five named graphs” the 5NG:

  1. scatterplots
  2. linegraphs
  3. boxplots
  4. histograms
  5. barplots

We’ll also present some variations of these plots, but with this basic repertoire of five graphics in your toolbox, you can visualize a wide array of different variable types. Note that certain plots are only appropriate for categorical variables while others are only appropriate for quantitative variables.

2.3 5NG#1: Scatterplots

The simplest of the 5NG are scatterplots, also called bivariate plots. They allow you to visualize the relationship between two numerical variables. While you may already be familiar with scatterplots, let’s view them through the lens of the Grammar of Graphics we presented in Section 2.1. Specifically, we will visualize the relationship between the following two numerical variables in the flights data frame included in the nycflights13 package:

  1. dep_delay: departure delay on the horizontal “x” axis and
  2. arr_delay: arrival delay on the vertical “y” axis

for Alaska Airlines flights leaving NYC in 2013. This requires paring down the data from all 336,776 flights that left NYC in 2013, to only the 714 Alaska Airlines flights that left NYC in 2013. We do this so our scatterplot will involve a manageable 714 points, and not an overwhelmingly large number like 336,776. To achieve this, we’ll take the flights data frame, filter the rows so that only the 714 rows corresponding to Alaska Airlines flights are kept, and save this in a new data frame called alaska_flights using the <- assignment operator :

For now we suggest you don’t worry if you don’t fully understand this code. We’ll see later in Chapter 3 on data wrangling that this code uses the dplyr package for data wrangling to achieve our goal: it takes the flights data frame and filter it to only return the rows where carrier is equal to "AS", Alaska Airlines’ carrier code. Recall from Section 1.2 that testing for equality is specified with == and not =.

For now however, convince yourself that this code achieves what it is supposed to by exploring the resulting data frame by running View(alaska_flights). You’ll see that it has 714 rows, consisting of only 714 Alaska Airlines flights.

Learning check

(LC2.1) Take a look at both the flights and alaska_flights data frames by running View(flights) and View(alaska_flights). In what respect do these data frames differ? For example, think about the number of rows in each dataset.

2.3.1 Scatterplots via geom_point

Let’s now go over the code that will create the desired scatterplot, while keeping in the Grammar of Graphics we introduced in Section 2.1. Let’s take a look at the code and break it down piece-by-piece.

Within the ggplot() function, we specify two of the components of the Grammar of Graphics as arguments (i.e. inputs):

  1. The data to be the alaska_flights data frame by setting data = alaska_flights.
  2. The aesthetic mapping by setting mapping = aes(x = dep_delay, y = arr_delay). Specifically, the variable dep_delay maps to the x position aesthetic while the variable arr_delay maps to the y position aesthetic.

We then add a layer to the ggplot() function call using the + sign. The added layer in question specifies the third component of the grammar: the geometric object. In this case the geometric object is set to be points by specifying geom_point().

After running these two lines of code in your console, you’ll notice two outputs: the graphic shown in Figure 2.2 and a warning message.

Warning: Removed 5 rows containing missing values (geom_point).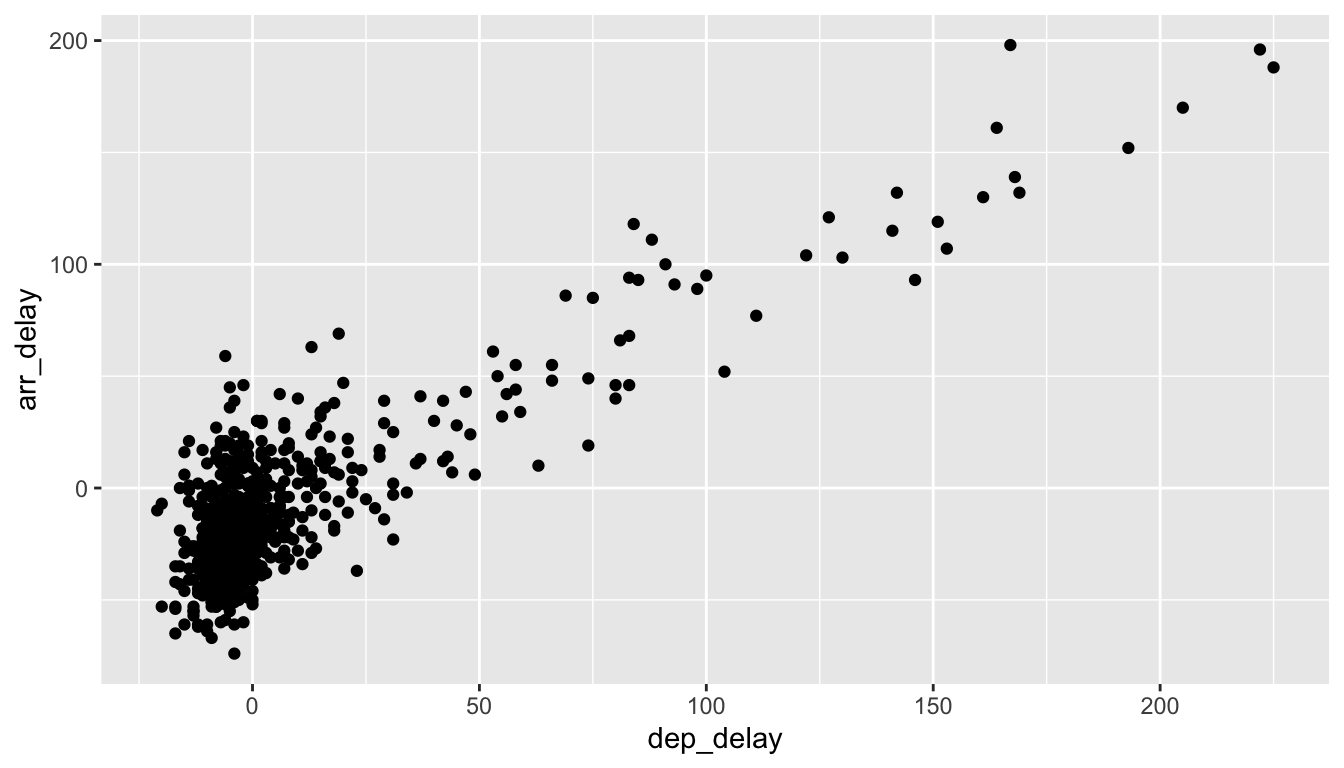
Arrival delays vs departure delays for Alaska Airlines flights from NYC in 2013.

FIGURE 2.2: Arrival delays vs departure delays for Alaska Airlines flights from NYC in 2013.

Let’s first unpack the graphic in Figure 2.2. Observe that a positive relationship exists between dep_delay and arr_delay: as departure delays increase, arrival delays tend to also increase. Observe also the large mass of points clustered near (0, 0), the point indicating flights that neither departed nor arrived late.

Let’s turn our attention to the warning message. R is alerting us to the fact that 5 rows were ignored due to them being missing. For these 5 rows, either the value for dep_delay or arr_delay or both were missing (recorded in R as NA), and thus these rows were ignored in our plot.

Before we continue, let’s make a few more observations about this code that created the scatterplot. Note that the + sign comes at the end of lines, and not at the beginning. You’ll get an error in R if you put it at the beginning of a line. When adding layers to a plot, you are encouraged to start a new line after the + (by pressing the Return/Enter button on your keyboard) so that the code for each layer is on a new line. As we add more and more layers to plots, you’ll see this will greatly improve the legibility of your code.

To stress the importance of adding the layer specifying the geometric object, consider Figure 2.3 where no layers are added. Because the geometric object was not specified, we have a blank plot which is not very useful!

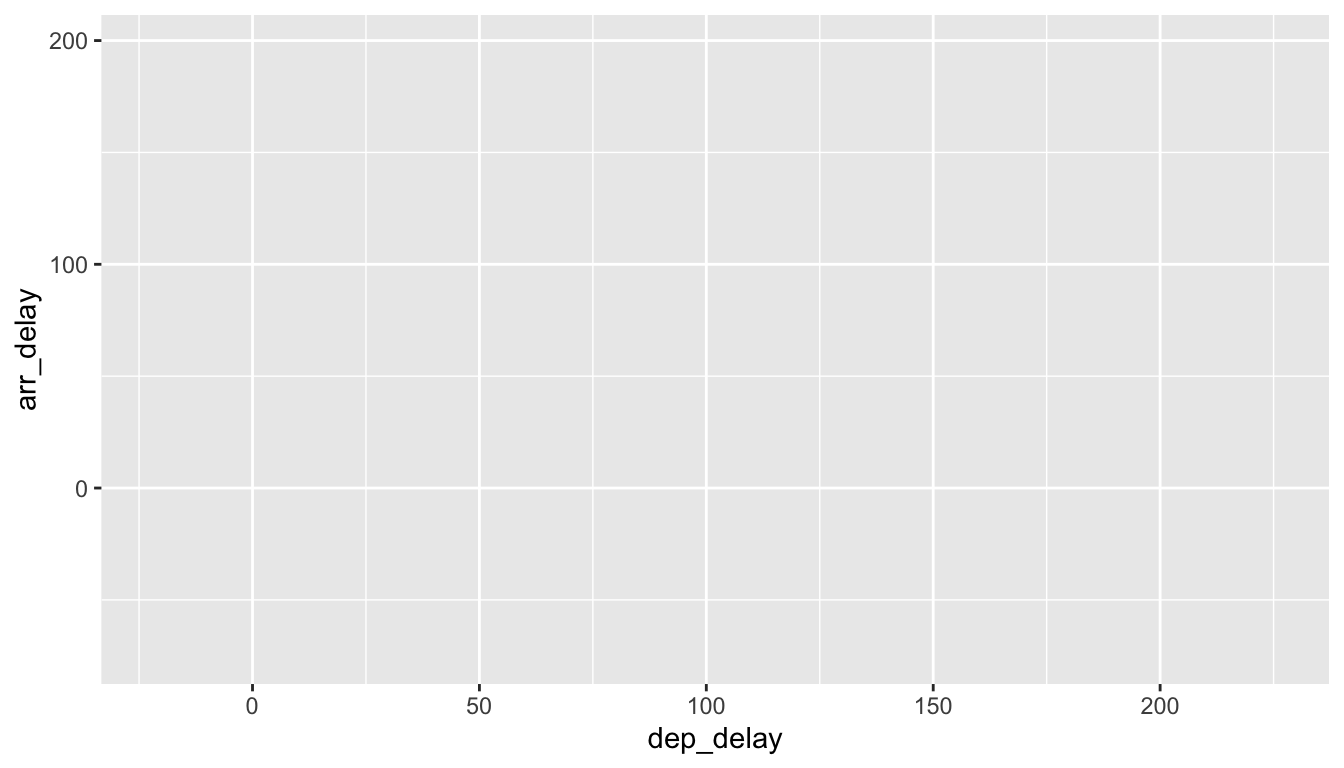
A plot with no layers.

FIGURE 2.3: A plot with no layers.

Learning check

(LC2.2) What are some practical reasons why dep_delay and arr_delay have a positive relationship?

(LC2.3) What variables in the weather data frame would you expect to have a negative correlation (i.e. a negative relationship) with dep_delay? Why? Remember that we are focusing on numerical variables here. Hint: Explore the weather dataset by using the View() function.

(LC2.4) Why do you believe there is a cluster of points near (0, 0)? What does (0, 0) correspond to in terms of the Alaskan flights?

(LC2.5) What are some other features of the plot that stand out to you?

(LC2.6) Create a new scatterplot using different variables in the alaska_flights data frame by modifying the example given.

2.3.2 Over-plotting

The large mass of points near (0, 0) in Figure 2.2 can cause some confusion since it is hard to tell the true number of points that are plotted. This is the result of a phenomenon called overplotting. As one may guess, this corresponds to points being plotted on top of each other over and over again. When overplotting occurs, it is difficult to know the number of points being plotted. There are two methods to address the issue of overplotting. Either by

  1. Adjusting the transparency of the points or
  2. Adding a little random “jitter”, or random “nudges”, to each of the points.

Method 1: Changing the transparency

The first way of addressing overplotting is to change the transparency/opacity of the points by setting the alpha argument in geom_point(). We can change the alpha argument to be any value between 0 and 1, where 0 sets the points to be 100% transparent and 1 sets the points to be 100% opaque. By default, alpha is set to 1. In other words, if we don’t explicitly set an alpha value, R will use alpha = 1.

Note how the following code is identical to the code in Section 2.3 that created the scatterplot with overplotting, but with alpha = 0.2 added to the geom_point():

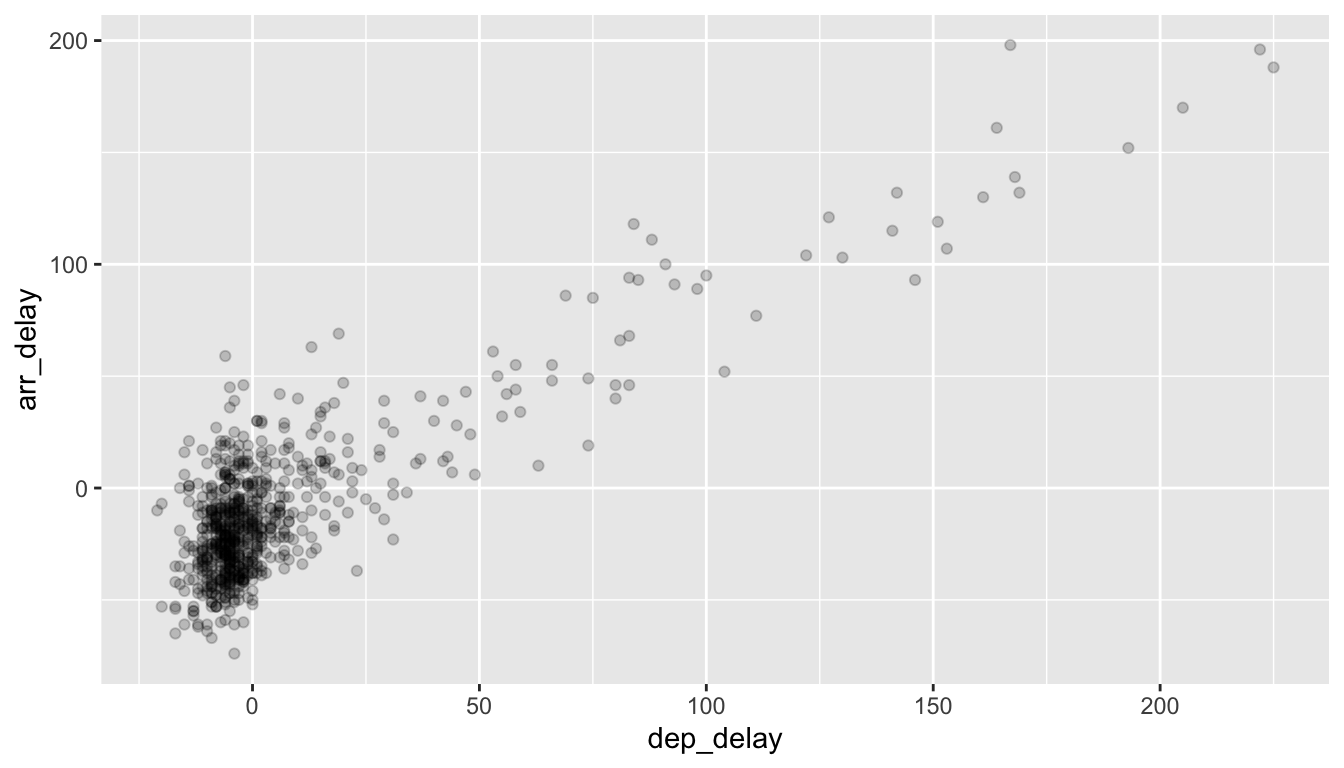
Arrival vs departure delays scatterplot with alpha = 0.2.

FIGURE 2.4: Arrival vs departure delays scatterplot with alpha = 0.2.

The key feature to note in Figure 2.4 is that the transparency of the points is cumulative: areas with a high-degree of overplotting are darker, whereas areas with a lower degree are less dark. Note furthermore that there is no aes() surrounding alpha = 0.2. This is because we are not mapping a variable to an aesthetic attribute, but rather merely changing the default setting of alpha. In fact, you’ll receive an error if you try to change the second line to read geom_point(aes(alpha = 0.2)).

Method 2: Jittering the points

The second way of addressing overplotting is by jittering all the points, in other words give each point a small “nudge” in a random direction. You can think of “jittering” as shaking the points around a bit on the plot. Let’s illustrate using a simple example first. Say we have a data frame with 4 identical rows of x & y values: (0,0), (0,0), (0,0), and (0,0). In Figure 2.5, we present both the regular scatterplot of these 4 points (on the left) and its jittered counterpart (on the right).

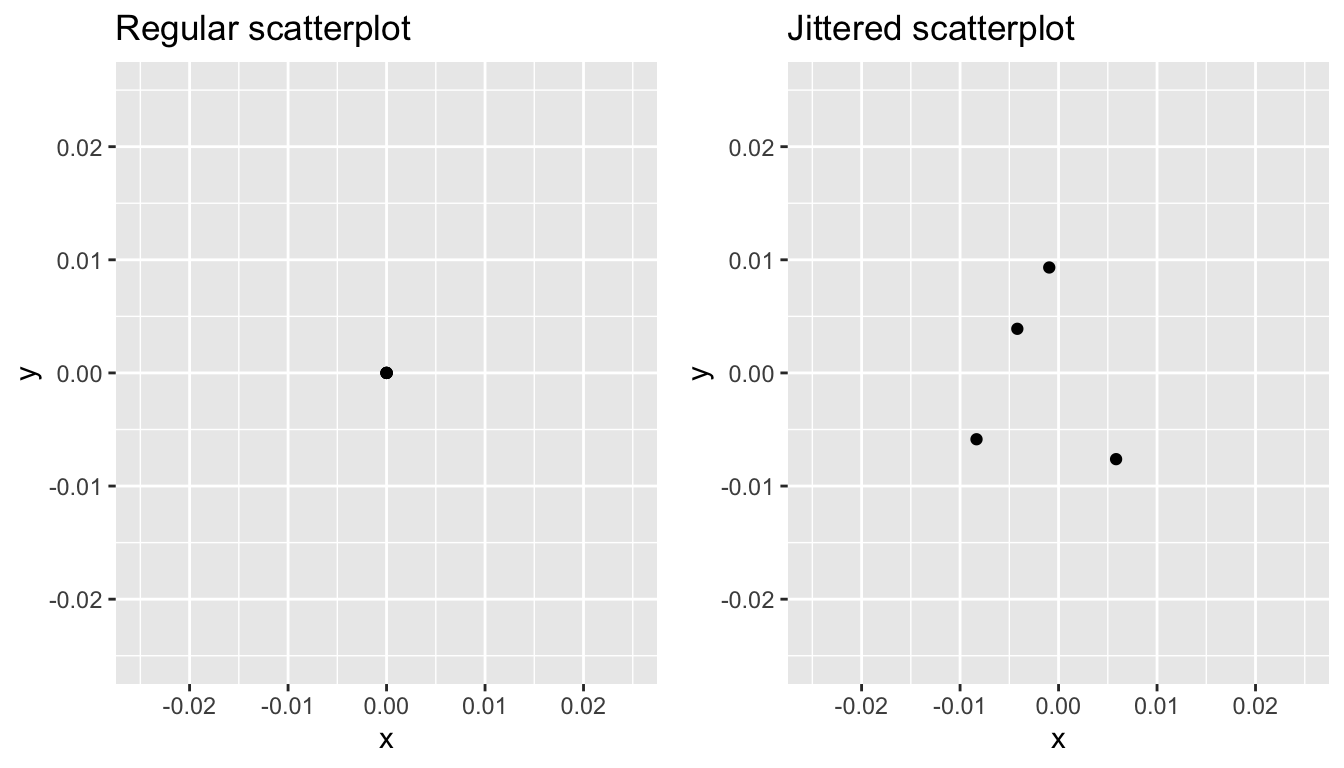
Regular and jittered scatterplot.

FIGURE 2.5: Regular and jittered scatterplot.

In the left-hand regular scatterplot, observe that the 4 points are superimposed on top of each other. While we know there are 4 values being plotted, this fact might not be apparent to others. In the right-hand jittered scatterplot, observe that since each point is given a random “nudge”, it is now plainly evident that this plot involves four points.

Keep in mind however that jittering is strictly a visualization tool; even after creating a jittered scatterplot, the original values saved in the data frame remain unchanged.

To create a jittered scatterplot, instead of using geom_point(), we use geom_jitter(). Observe how the following code is very similar to the code that created the scatterplot with overplotting in Subsection 2.3.1, but with geom_point() replaced with geom_jitter().

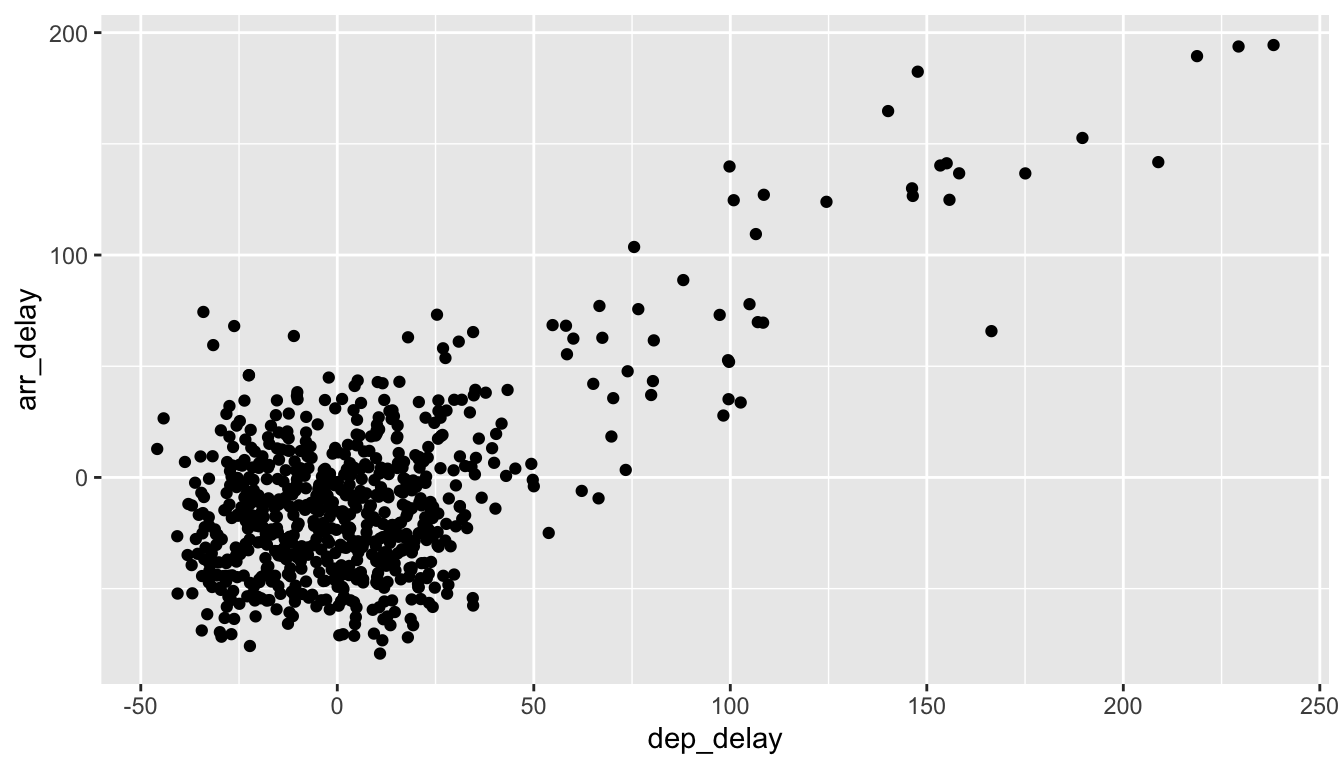
Arrival vs departure delays jittered scatterplot.

FIGURE 2.6: Arrival vs departure delays jittered scatterplot.

In order to specify how much jitter to add, we adjusted the width and height arguments to geom_jitter(). This corresponds to how hard you’d like to shake the plot in horizontal x-axis units and vertical y-axis units respectively. In this case, both axes are in minutes. How much jitter should we add using the width and height arguments? On the one hand, it is important to add just enough jitter to break any overlap in points, but on the other hand, not so much that we completely alter the original pattern in points.

As can be seen in the resulting Figure 2.6, in this case jittering doesn’t really provide much new insight. In this particular case, it can be argued that changing the transparency of the points by setting alpha proved more effective. When would it be better to use a jittered scatterplot? When would it be better to alter the points’ transparency? There is no single right answer that applies to all situations. You need to make a subjective choice and own that choice. At the very least when confronted with overplotting however, we suggest you make both types of plots and see which one better emphasizes the point you are trying to make.

Learning check

(LC2.7) Why is setting the alpha argument value useful with scatterplots? What further information does it give you that a regular scatterplot cannot?

(LC2.8) After viewing Figure 2.4, give an approximate range of arrival delays and departure delays that occur the most frequently. How has that region changed compared to when you observed the same plot without the alpha = 0.2 set in Figure 2.2?

2.3.3 Summary

Scatterplots display the relationship between two numerical variables. They are among the most commonly used plots because they can provide an immediate way to see the trend in one numerical variable versus another. However, if you try to create a scatterplot where either one of the two variables is not numerical, you might get strange results. Be careful!

With medium to large datasets, you may need to play around with the different modifications to scatterplots we saw such as changing the transparency/opacity of the points or by jittering the points. This tweaking is often a fun part of data visualization, since you’ll have the chance to see different relationships emerge as you tinker with your plots.

2.4 5NG#2: Linegraphs

The next of the five named graphs are linegraphs. Linegraphs show the relationship between two numerical variables when the variable on the x-axis, also called the explanatory variable, is of a sequential nature. In other words there is an inherent ordering to the variable. The most common example of linegraphs have some notion of time on the x-axis: hours, days, weeks, years, etc. Since time is sequential, we connect consecutive observations of the variable on the y-axis with a line. Linegraphs that have some notion of time on the x-axis are also called time series plots. Let’s illustrate linegraphs using another data set in the nycflights13 package: the weather data frame.

Let’s explore the weather data frame by running View(weather) and glimpse(weather) and furthermore let’s read the associated help file by running ?weather to bring up the help file.

Observe that there is a variable called temp of hourly temperature recordings in Fahrenheit at weather stations near all three airports in New York City: Newark (origin code EWR), John F. Kennedy International, and La Guardia (LGA). However, instead of considering hourly temperatures for all days in 2013 for all three airports, for simplicity let’s only consider hourly temperatures at Newark airport for the first 15 days in January.

Recall in Section 2.3 we used the filter() function to only choose the subset of rows of flights corresponding to Alaska Airlines flights. We similarly use filter() here, but by using the & operator we only choose the subset of rows of weather where the origin is "EWR", the month is January, and the day is between 1 and 15. Recall we performed a similar task in Section 2.3 when creating the alaska_flights data frame of only Alaska Airlines flights, a topic we’ll explore more in Chapter 3 on data wrangling.

Learning check

(LC2.9) Take a look at both the weather and early_january_weather data frames by running View(weather) and View(early_january_weather). In what respect do these data frames differ?

(LC2.10) View() the flights data frame again. Why does the time_hour variable uniquely identify the hour of the measurement whereas the hour variable does not?

2.4.1 Linegraphs via geom_line

Let’s create a time series plot of the hourly temperatures saved in the early_january_weather data frame by using geom_line() to create a linegraph, instead of using geom_point() like we used previously to create scatterplots:

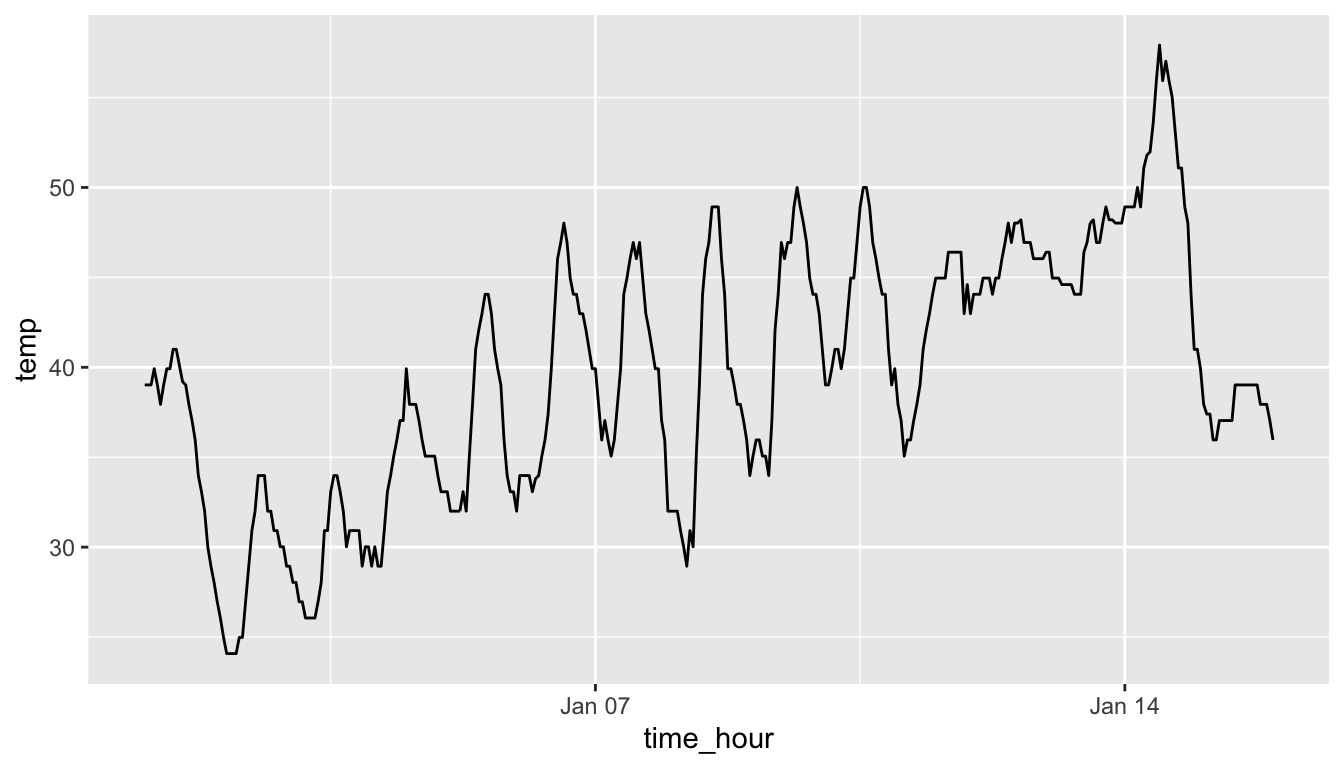
Hourly temperature in Newark for January 1-15, 2013.

FIGURE 2.7: Hourly temperature in Newark for January 1-15, 2013.

Much as with the ggplot() code that created the scatterplot of departure and arrival delays for Alaska Airlines flights in Figure 2.2, let’s break down this code piece-by-piece in terms of the Grammar of Graphics:

Within the ggplot() function call, we specify two of the components of the Grammar of Graphics as arguments:

  1. The data to be the early_january_weather data frame by setting data = early_january_weather.
  2. The aesthetic mapping by setting mapping = aes(x = time_hour, y = temp). Specifically, the variable time_hour maps to the x position aesthetic while the variable temp maps to the y position aesthetic.

We add a layer to the ggplot() function call using the + sign. The layer in question specifies the third component of the grammar: the geometric object in question. In this case the geometric object is a line, set by specifying geom_line().

Learning check

(LC2.11) Why should linegraphs be avoided when there is not a clear ordering of the horizontal axis?

(LC2.12) Why are linegraphs frequently used when time is the explanatory variable on the x-axis?

(LC2.13) Plot a time series of a variable other than temp for Newark Airport in the first 15 days of January 2013.

2.4.2 Summary

Linegraphs, just like scatterplots, display the relationship between two numerical variables. However it is preferred to use linegraphs over scatterplots when the variable on the x-axis (i.e. the explanatory variable) has an inherent ordering, such as some notion of time.

2.5 5NG#3: Histograms

Let’s consider the temp variable in the weather data frame once again, but unlike with the linegraphs in Section 2.4, let’s say we don’t care about its relationship with time, but rather we only care about how the values of temp distribute. In other words:

  1. What are the smallest and largest values?
  2. What is the “center” or “most typical” value?
  3. How do the values spread out?
  4. What are frequent and infrequent values?

One way to visualize this distribution of this single variable temp is to plot them on a horizontal line as we do in Figure 2.8:

Plot of hourly temperature recordings from NYC in 2013.

FIGURE 2.8: Plot of hourly temperature recordings from NYC in 2013.

This gives us a general idea of how the values of temp distribute: observe that temperatures vary from around 11°F (-11°C) up to 100°F (38°C). Furthermore, there appear to be more recorded temperatures between 40°F and 60°F than outside this range. However, because of the high degree of overplotting in the points, it’s hard to get a sense of exactly how many values are between say 50°F and 55°F.

What is commonly produced instead of Figure 2.8 is known as a histogram. A histogram is a plot that visualizes the distribution of a numerical value as follows:

  1. We first cut up the x-axis into a series of bins, where each bin represents a range of values.
  2. For each bin, we count the number of observations that fall in the range corresponding to that bin.
  3. Then for each bin, we draw a bar whose height marks the corresponding count.

Let’s drill-down on an example of a histogram, shown in Figure 2.9.

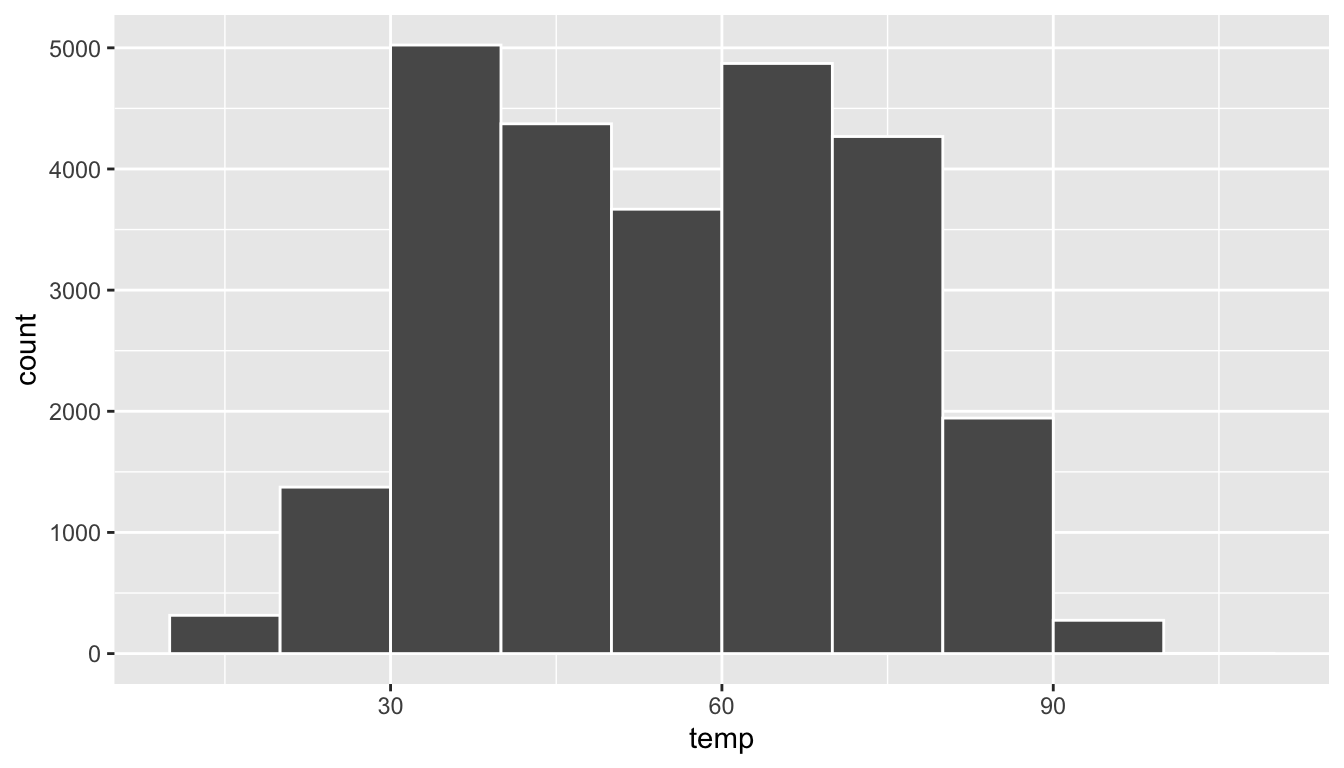
Example histogram.

FIGURE 2.9: Example histogram.

Let’s focus only on temperatures between 30°F (-1°C) and 60°F (15°C) for now. Observe that there are three bins of equal width between 30 and 60°F. Thus we have three bins of width 10°F each: one bin for the 30-40°F range, another bin for the 40-50°F range, and another bin for the 50-60°F range. Since:

  1. The bin for the 30-40°F range has a height of around 5000. In other words, around 5000 of the hourly temperature recordings are between 30°F and 40°F.
  2. The bin for the 40-50°F range has a height of around 4300. In other words, around 4300 of the hourly temperature recordings are between 40°F and 50°F.
  3. The bin for the 50-60°F range has a height of around 3500. In other words, around 3500 of the hourly temperature recordings are between 50°F and 60°F.

All nine bins spanning 10°F to 100°F on the x-axis have this interpretation.

2.5.1 Histograms via geom_histogram

Let’s now present the ggplot() code to plot your first histogram! Unlike with scatterplots and linegraphs, there is now only one variable being mapped in aes(): the single numerical variable temp. The y-aesthetic of a histogram, the count of the observations in each bin, gets computed for you automatically. Furthermore, the geometric object layer is now a geom_histogram(). . After running the following code, you’ll see the histogram in Figure 2.10 as well as warning messages. We’ll discuss the warning messages first.

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Warning: Removed 1 rows containing non-finite values (stat_bin).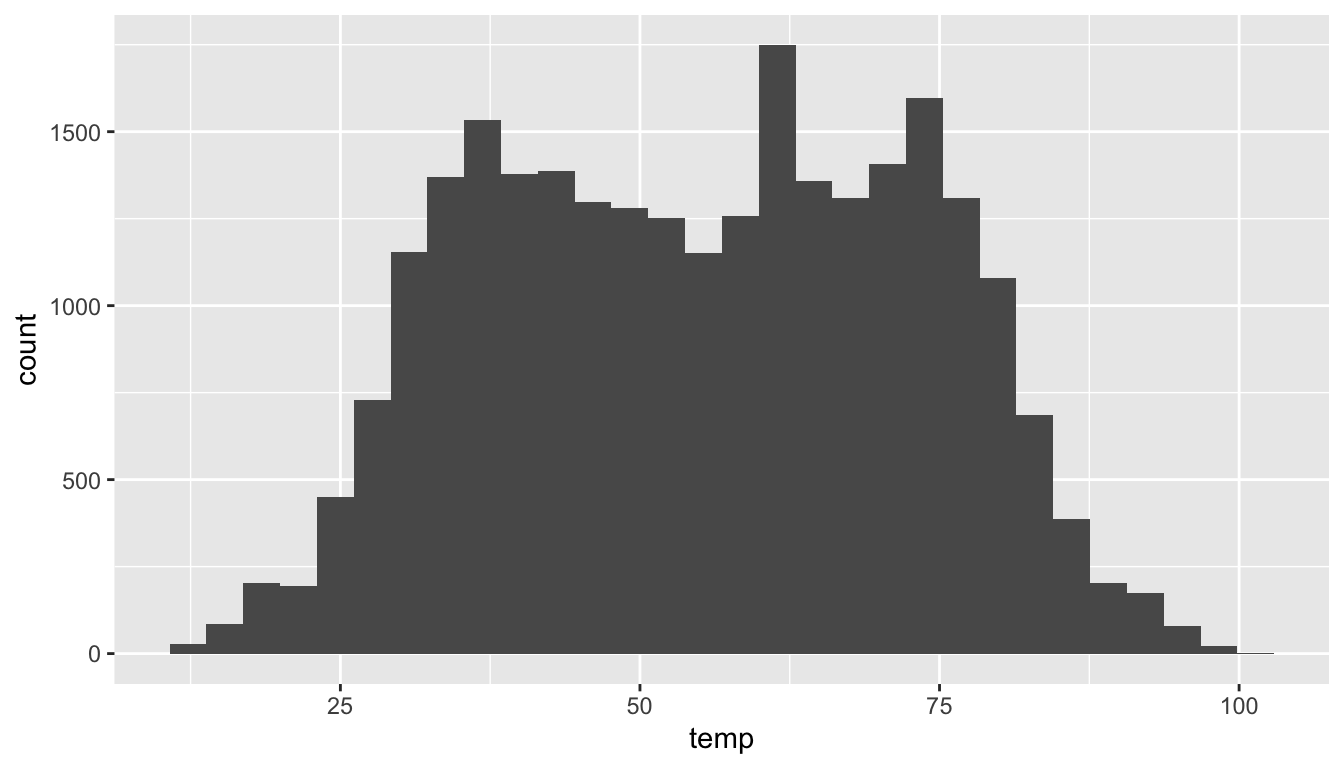
Histogram of hourly temperatures at three NYC airports.

FIGURE 2.10: Histogram of hourly temperatures at three NYC airports.

The first message is telling us that the histogram was constructed using bins = 30, in other words 30 equally spaced bins. This is known in computer programming as a default value; unless you override this default number of bins with a number you specify, R will choose 30 by default. We’ll see in the next section how to change the number of bins away from this default value.

The second message is telling us something similar to the warning message we received when we ran the code to create a scatterplot of departure and arrival delays for Alaska Airlines flights in Figure 2.2: that because one row has a missing NA value for temp, it was omitted from the histogram. R is just giving us a friendly heads up that this was the case.

Now let’s unpack the resulting histogram in Figure 2.10. Observe that values less than 25°F as well as values above 80°F are rather rare. However, because of the large number of bins, it’s hard to get a sense for which range of temperatures is spanned by each bin; everything is one giant amorphous blob. So let’s add white vertical borders demarcating the bins by adding a color = "white" argument to geom_histogram():

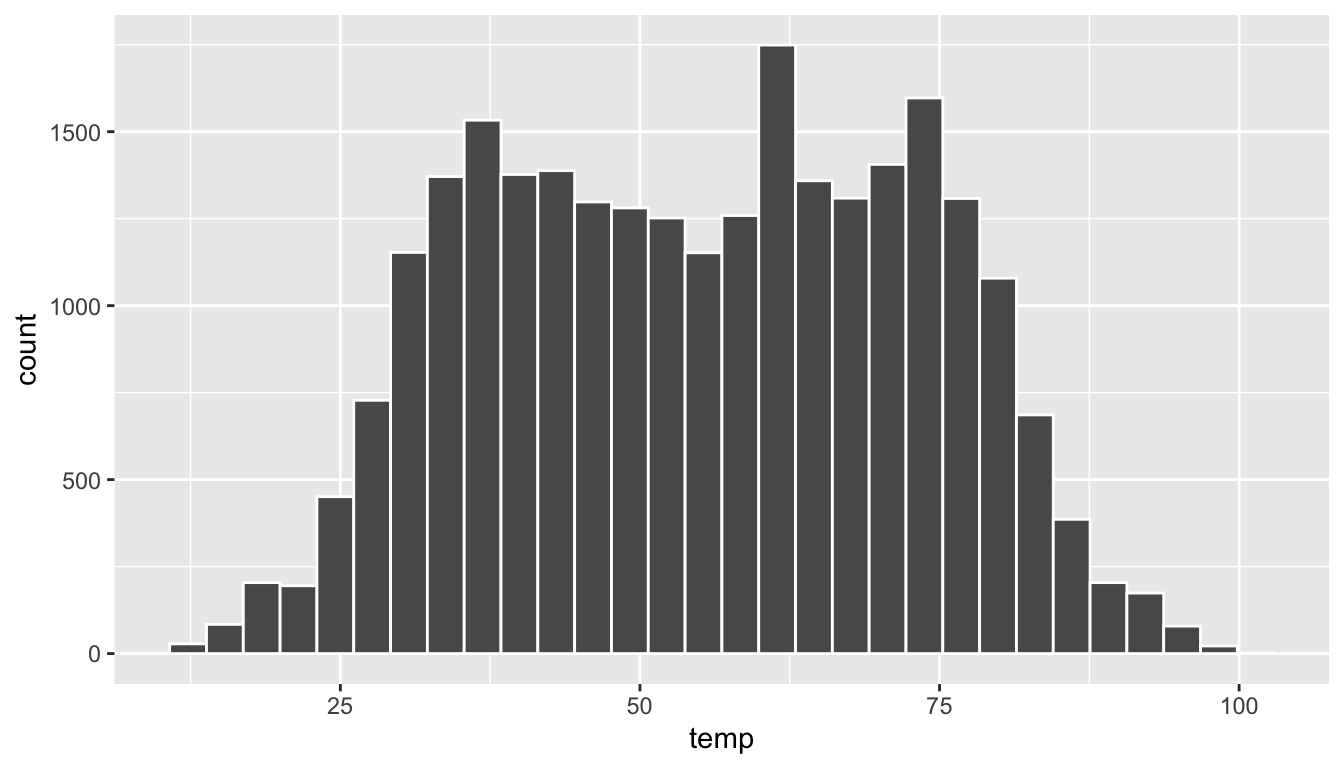
Histogram of hourly temperatures at three NYC airports with white borders.

FIGURE 2.11: Histogram of hourly temperatures at three NYC airports with white borders.

We now have an easier time associating ranges of temperatures to each of the bins in Figure 2.11. We can also vary the color of the bars by setting the fill argument. For example, you can set the bin colors to be “blue steel” by setting fill = "steelblue":

If you’re curious, run colors() to see all 657 possible choice of colors in R!

2.5.2 Adjusting the bins

Observe in Figure 2.11 that in the 50-75°F range there appear to be roughly 8 bins. Thus each bin has width 25 divided by 8, or roughly 3.12°F, which is not a very easily interpretable range to work with. Let’s improve this by adjusting the number of bins in our histogram in one of two ways:

  1. By adjusting the number of bins via the bins argument to geom_histogram().
  2. By adjusting the width of the bins via the binwidth argument to geom_histogram().

Using the first method, we have the power to specify how many bins we would like to cut the x-axis up in. As mentioned in the previous section, the default number of bins is 30. We can override this default, to say 40 bins, as follows:

Using the second method, instead of specifying the number of bins, we specify the width of the bins by using the binwidth argument in the geom_histogram() layer. For example, let’s set the width of each bin to be 10°F.

We compare both resulting histograms side-by-side in Figure 2.12.

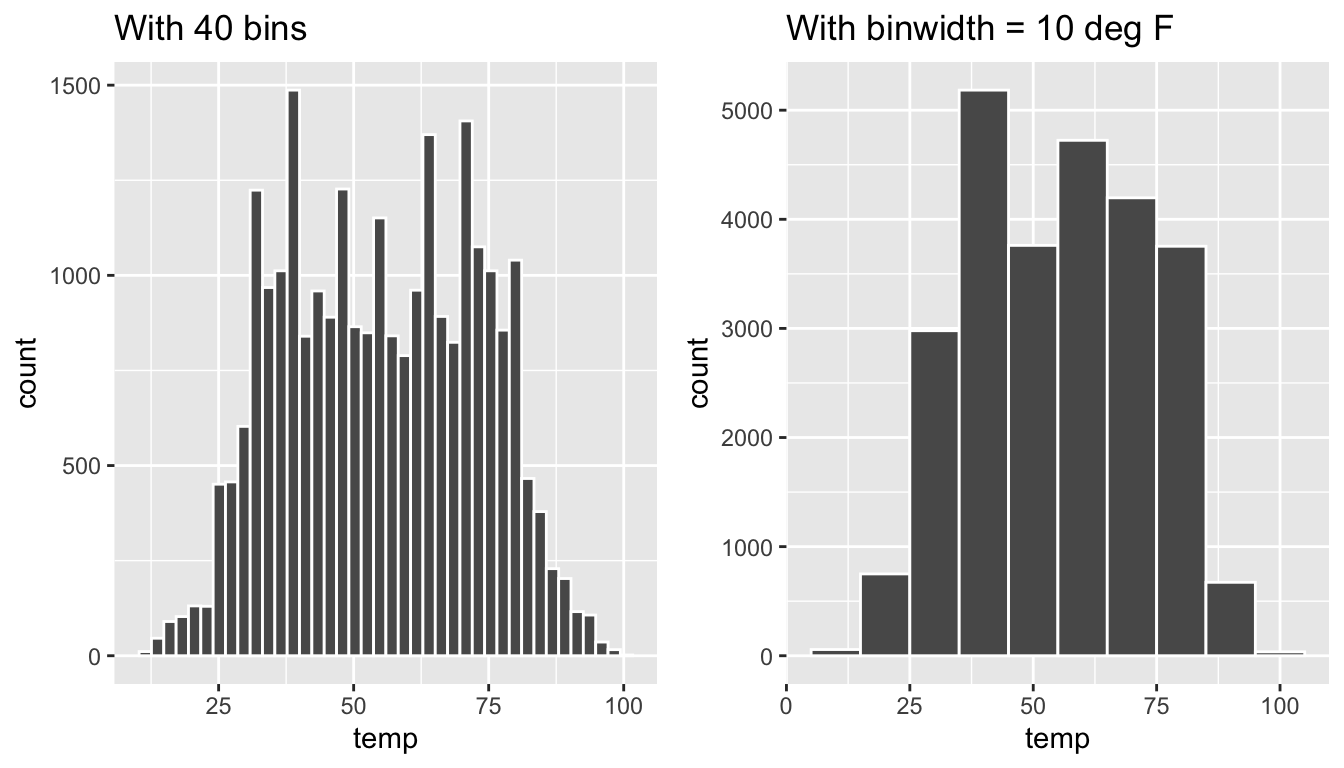
Setting histogram bins in two ways.

FIGURE 2.12: Setting histogram bins in two ways.

Learning check

(LC2.14) What does changing the number of bins from 30 to 40 tell us about the distribution of temperatures?

(LC2.15) Would you classify the distribution of temperatures as symmetric or skewed?

(LC2.16) What would you guess is the “center” value in this distribution? Why did you make that choice?

(LC2.17) Is this data spread out greatly from the center or is it close? Why?

2.5.3 Summary

Histograms, unlike scatterplots and linegraphs, present information on only a single numerical variable. Specifically, they are visualizations of the distribution of the numerical variable in question.

2.6 Facets

Before continuing the next of the 5NG, let’s briefly introduce a new concept called faceting. Faceting is used when we’d like to split a particular visualization by the values of another variable. This will create multiple copies of the same type of plot with matching x and y axes, but whose content will differ.

For example, suppose we were interested in looking at how the histogram of hourly temperature recordings at the three NYC airports we saw in Figure 2.9 differed in each month. We could “split” this histogram by the 12 possible months in a given year. In other words, we would plot histograms of temp for each month separately. We do this by adding facet_wrap(~ month) layer. Note the ~ is a “tilde” and can generally be found on the key next to the “1” key on US keyboards. The tilde is required and you’ll receive the error Error in as.quoted(facets) : object 'month' not found if you don’t include it here.

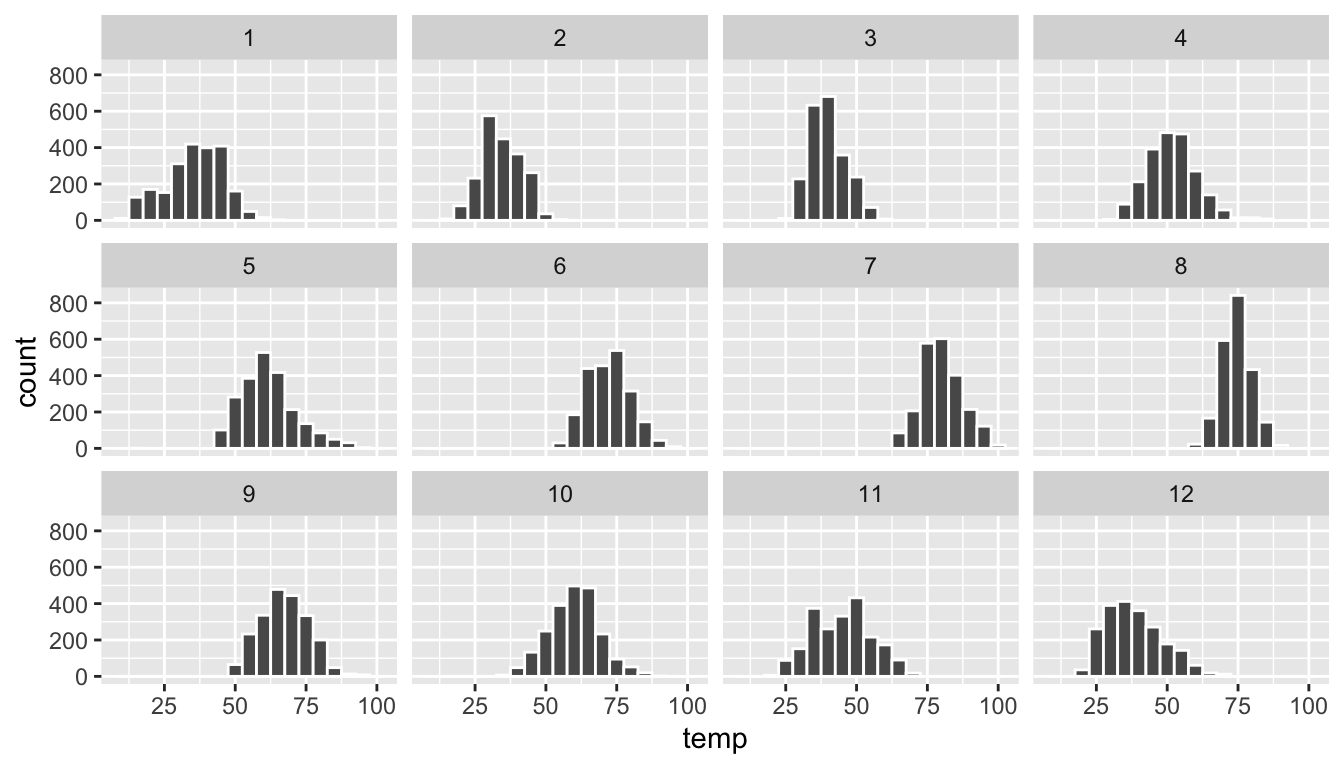
Faceted histogram of hourly temperatures by month.

FIGURE 2.13: Faceted histogram of hourly temperatures by month.

We can also specify the number of rows and columns in the grid by using the nrow and ncol arguments inside of facet_wrap(). For example, say we would like our faceted histogram to have 4 rows instead of 3. We simply add a nrow = 4 argument to facet_wrap(~ month)

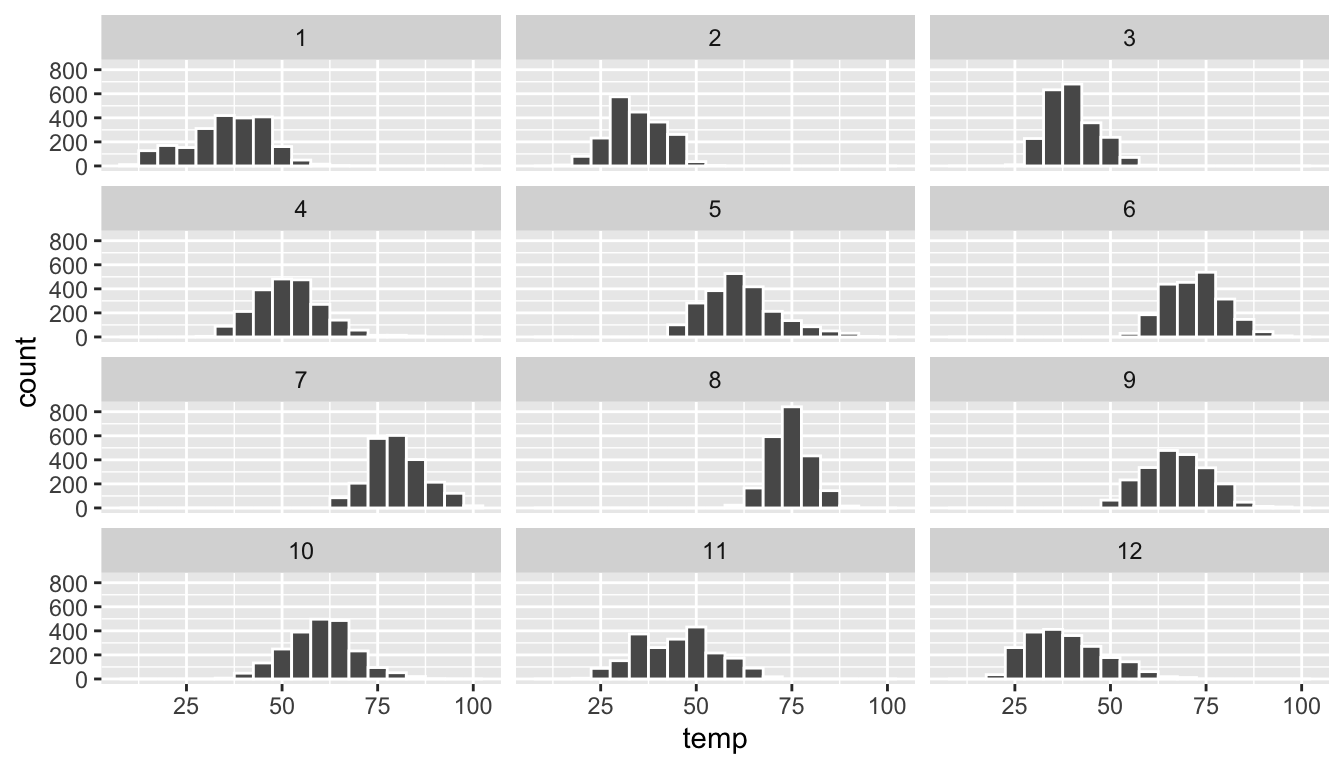
Faceted histogram with 4 instead of 3 rows.

FIGURE 2.14: Faceted histogram with 4 instead of 3 rows.

Observe in both Figures 2.13 and 2.14 that as we might expect in the Northern Hemisphere, temperatures tend to be higher in the summer months, while they tend to be lower in the winter.

Learning check

(LC2.18) What other things do you notice about this faceted plot? How does a faceted plot help us see relationships between two variables?

(LC2.19) What do the numbers 1-12 correspond to in the plot? What about 25, 50, 75, 100?

(LC2.20) For which types of datasets would these types of faceted plots not work well in comparing relationships between variables? Give an example describing the nature of these variables and other important characteristics.

(LC2.21) Does the temp variable in the weather data set have a lot of variability? Why do you say that?

2.7 5NG#4: Boxplots

While faceted histograms are one type of visualization used to compare the distribution of a numerical variable split by the values of another variable, another type of visualization that achieves this same goal are side-by-side boxplots. A boxplot is constructed from the information provided in the five-number summary of a numerical variable (see Appendix A.1).

To keep things simple for now, let’s only consider the 2141 hourly temperature recordings for the month of November, each represented as a point in Figure 2.15.

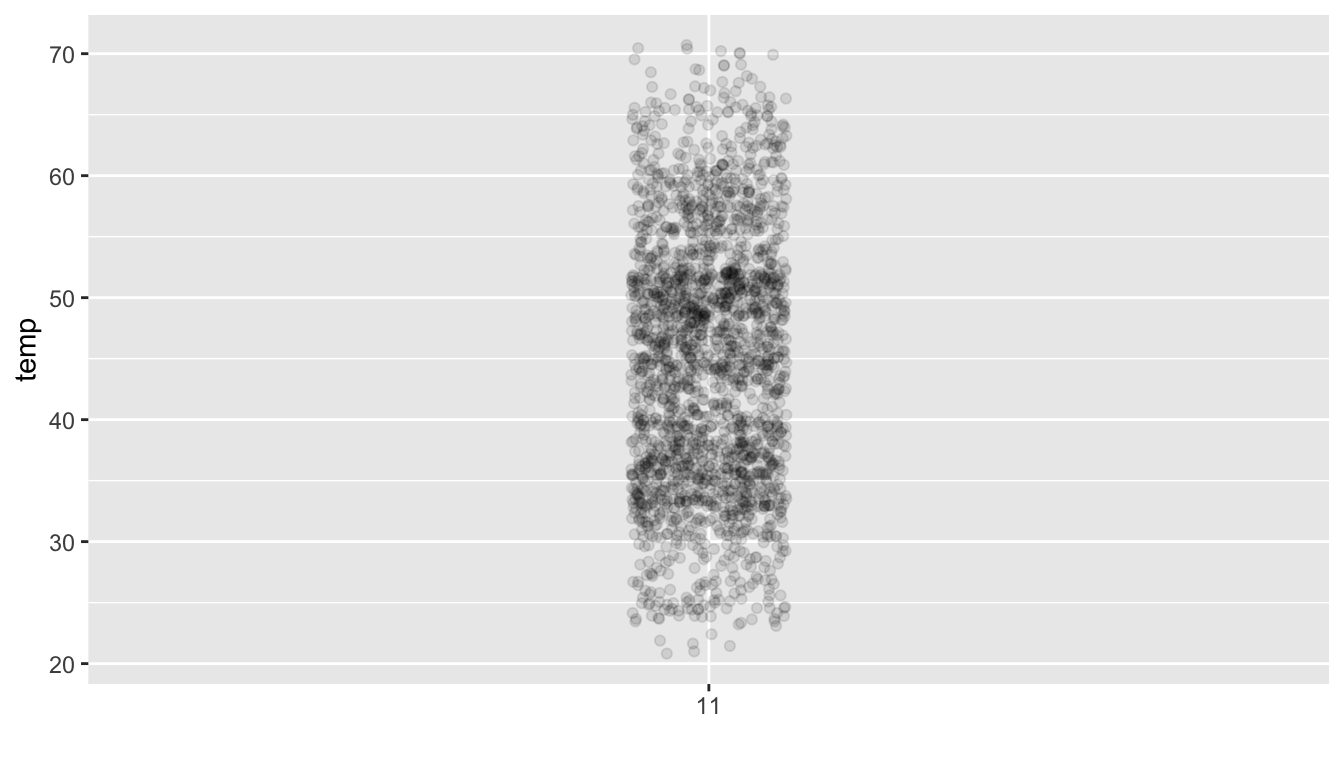
November temperatures represented as points.

FIGURE 2.15: November temperatures represented as points.

These 2141 observations have the following five-number summary:

  1. Minimum: 21°F
  2. First quartile AKA 25th percentile: 36°F
  3. Median AKA second quartile AKA 50th percentile: 45°F
  4. Third quartile AKA 75th percentile: 52°F
  5. Maximum: 71°F

In the left-most plot of Figure 2.16, let’s mark these 5 values with dashed horizontal lines on top of the 2141 points. In the middle plot of Figure 2.16 let’s add the boxplot. In the right-most plot of Figure 2.16, let’s remove the points and the dashed horizontal lines for clarity’s sake.

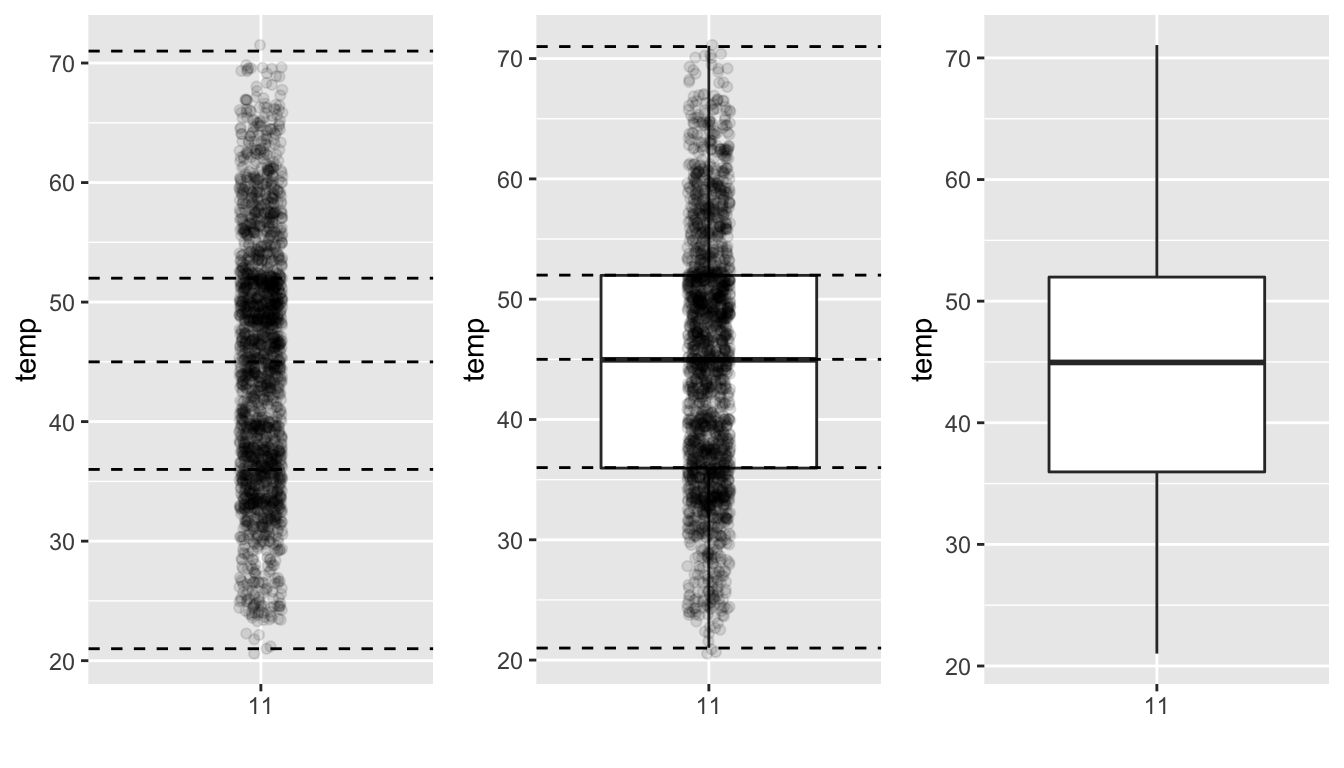
Building up a boxplot of November temperatures.

FIGURE 2.16: Building up a boxplot of November temperatures.

What the boxplot does is visually summarize the 2141 points by cutting the 2141 temperature recordings into quartiles at the dashed lines, where each quartile contains roughly 2141 \(\div\) 4 \(\approx\) 535 observations. Thus

  1. 25% of points fall below the bottom edge of the box, which is the first quartile of 36°F. In other words 25% of observations were colder than 36°F.
  2. 25% of points fall between the bottom edge of the box and the solid middle line, which is the median of 45°F. In other words 25% of observations were between 36 and 45°F and 50% of observations were colder than 45°F.
  3. 25% of points fall between the solid middle line and the top edge of the box, which is the third quartile of 52°F. In other words 25% of observations were between 45 and 52°F and 75% of observations were colder than 52°F.
  4. 25% of points fall above the top edge of the box. In other words 25% of observations were warmer than 52°F.
  5. The middle 50% of points lie within the interquartile range (IQR) between the first and third quartile of 52 - 36 = 16°F. The interquartile range is a measure of a numerical variable’s spread.

Furthermore, in the right-most plot of Figure 2.16, we see the whiskers of the boxplot. The whiskers stick out from either end of the box all the way to the minimum and maximum observed temperatures of 21°F and 71°F respectively. However, the whiskers don’t always extend to the smallest and largest observed values as they do here. They in fact extend no more than 1.5 \(\times\) the interquartile range from either end of the box. In this case of the November temperatures, no more than 1.5 \(\times\) 16°F = 24°F from either end of the box. Any observed values outside this range get marked with points called outliers, which we’ll see in the next section.

2.7.1 Boxplots via geom_boxplot

Let’s now create a side-by-side boxplot of hourly temperatures split by the 12 months as we did previously with the faceted histograms. We do this by mapping the month variable to the x-position aesthetic, the temp variable to the y-position aesthetic, and by adding a geom_boxplot() layer:

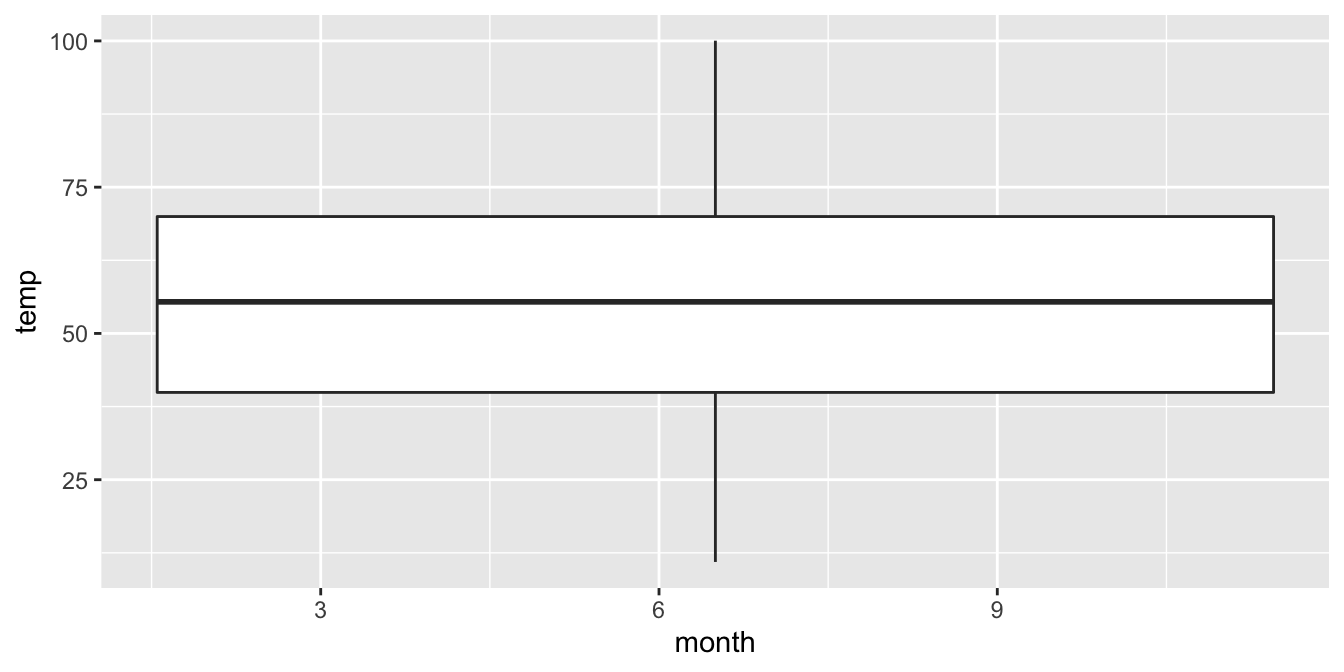
Invalid boxplot specification.

FIGURE 2.17: Invalid boxplot specification. 

Warning messages:
1: Continuous x aesthetic -- did you forget aes(group=...)? 
2: Removed 1 rows containing non-finite values (stat_boxplot).

Observe in Figure 2.17 that this plot does not provide information about temperature separated by month. The first warning message clues us in as to why. It is telling us that we have a “continuous”, or numerical variable, on the x-position aesthetic. Boxplots however require a categorical variable to be mapped to the x-position aesthetic. The second warning message is identical to the warning message when plotting a histogram of hourly temperatures: that one of the values was recorded as NA missing.

We can convert the numerical variable month into a categorical variable by using the factor() function. So after applying factor(month), month goes from having numerical values 1, 2, …, and 12 to having labels “1”, “2”, …, and “12.”

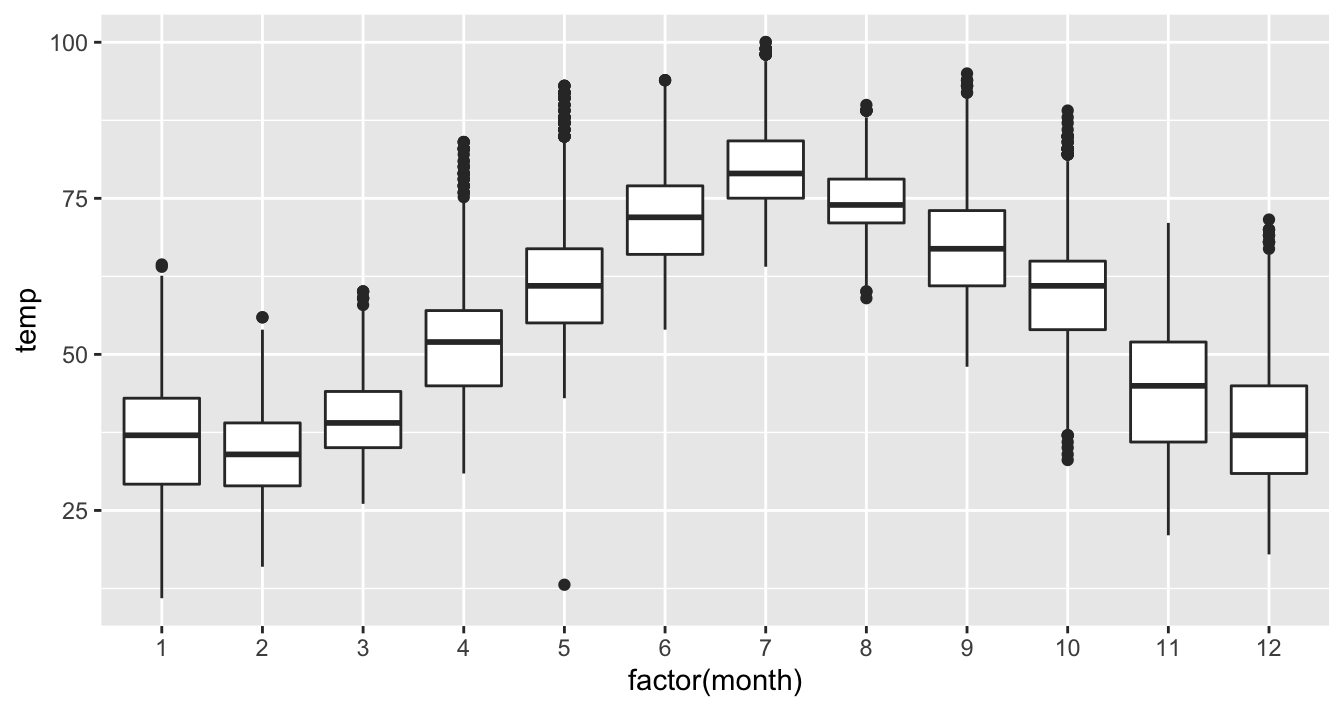
Side-by-side boxplot of temperature split by month.

FIGURE 2.18: Side-by-side boxplot of temperature split by month.

The resulting Figure 2.18 shows 12 separate “box and whiskers” plots similar to the right-most plot of Figure 2.16 focusing only on November:

  • The “box” portions of the visualization represent the 1st quartile, the median AKA the 2nd quartile, and the 3rd quartile.
  • The height of each box, i.e. the value of the 3rd quartile minus the value of the 1st quartile, is the interquartile range (IQR). It is a measure of the spread of the middle 50% of values, with longer boxes indicating more variability.
  • The “whisker” portions of these plots extend out from the bottoms and tops of the boxes and represent points less than the 25th percentile and greater than the 75th percentiles respectively. They’re set to extend out no more than \(1.5 \times IQR\) units away from either end of the boxes. We say “no more than” because the ends of the whiskers have to correspond to observed temperatures. The length of these whiskers show how the data outside the middle 50% of values vary, with longer whiskers indicating more variability.
  • The dots representing values falling outside the whiskers are called outliers. These can be thought of as anomalous values.

It is important to keep in mind that the definition of an outlier is somewhat arbitrary and not absolute. In this case, they are defined by the length of the whiskers, which are no more than \(1.5 \times IQR\) units long. Looking at this plot we can see, as expected, that summer months (6 through 8) have higher median temperatures as evidenced by the higher solid lines in the middle of the boxes. We can easily compare temperatures across months by drawing imaginary horizontal lines across the plot. Furthermore, the height of the 12 boxes as quantified by the interquartile ranges are informative too; they tell us about variability, or spread, of temperatures recorded in a given month.

Learning check

(LC2.22) What does the dot at the bottom of the plot for May correspond to? Explain what might have occurred in May to produce this point.

(LC2.23) Which months have the highest variability in temperature? What reasons can you give for this?

(LC2.24) We looked at the distribution of the numerical variable temp split by the numerical variable month that we converted to a categorical variable using the factor() function. Why would a boxplot of temp split by the numerical variable pressure similarly converted to a categorical variable using the factor() not be informative?

(LC2.25) Boxplots provide a simple way to identify outliers. Why may outliers be easier to identify when looking at a boxplot instead of a faceted histogram?

2.7.2 Summary

Side-by-side boxplots provide us with a way to compare the distribution of a numerical variable across multiple values of another variable. One can see where the median falls across the different groups by looking at the solid line in the center of the boxes. To study the spread of a numerical variable within one of the boxes, look at both the length of the box and also how far the whiskers extend from either end of the box. Outliers are even more easily identified when looking at a boxplot than when looking at a histogram as they are marked with distinct points.

2.8 5NG#5: Barplots

Both histograms and boxplots are tools to visualize the distribution of numerical variables. Another common task is to visualize the distribution of a categorical variable. This is a simpler task, as we are simply counting different categories of a categorical variable, also known as the levels of the categorical variable. Often the best way to visualize these different counts, also known as frequencies, is with barplots (also called barcharts).

One complication, however, is how your data is represented. Is the categorical variable of interest “pre-counted” or not? For example, run the following code that manually creates two data frames representing a collection of fruit: 3 apples and 2 oranges.

We see both the fruits and fruits_counted data frames represent the same collection of fruit. Whereas fruits just lists the fruit individually…

# A tibble: 5 x 1
  fruit 
  <chr> 
1 apple 
2 apple 
3 orange
4 apple 
5 orange

… fruits_counted has a variable count which represent the “pre-counted” values of each fruit.

# A tibble: 2 x 2
  fruit  number
  <chr>   <dbl>
1 apple       3
2 orange      2

Depending on how your categorical data is represented, you’ll need to add a different geometric layer type to your ggplot() to create a barplot, as we now explore.

2.8.1 Barplots via geom_bar or geom_col

Let’s generate barplots using these two different representations of the same basket of fruit: 3 apples and 2 oranges. Using the fruits data frame where all 5 fruit are listed individually in 5 rows, we map the fruit variable to the x-position aesthetic and add a geom_bar() layer:

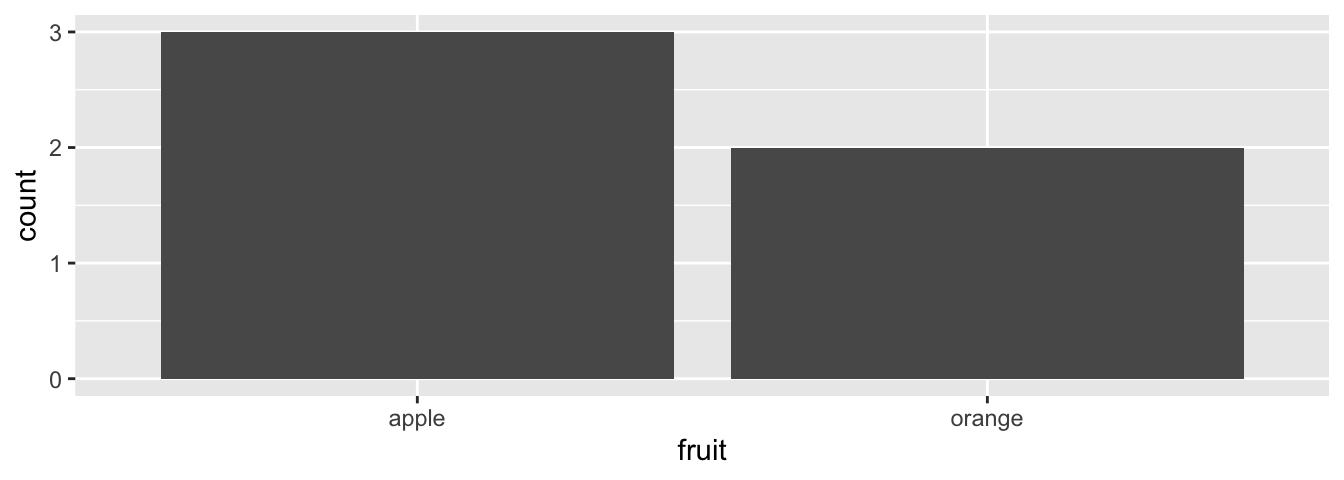
Barplot when counts are not pre-counted.

FIGURE 2.19: Barplot when counts are not pre-counted.

However, using the fruits_counted data frame where the fruit have been “pre-counted”, we once again map the fruit variable to the x-position aesthetic, but here we also map the count variable to the y-position aesthetic, and add a geom_col() layer instead.

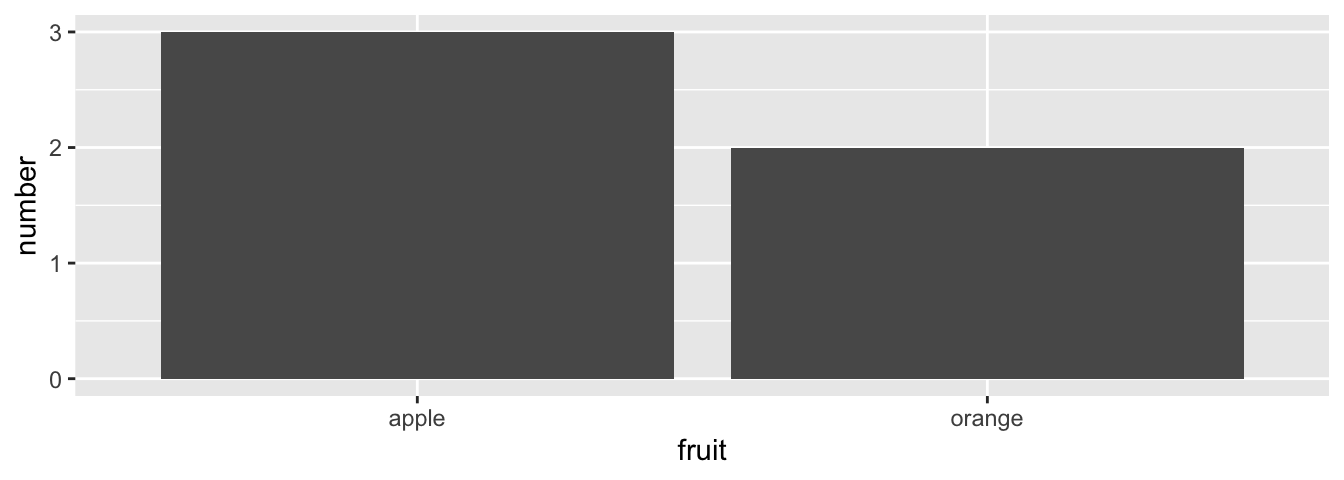
Barplot when counts are pre-counted.

FIGURE 2.20: Barplot when counts are pre-counted.

Compare the barplots in Figures 2.19 and 2.20. They are identical because they reflect counts of the same five fruit. However depending on how our categorical data is represented, either “pre-counted” or not, we must add a different geom layer. When the categorical variable whose distribution you want to visualize

  • Is not pre-counted in your data frame, we use geom_bar().
  • Is pre-counted in your data frame, we use geom_col() with the y-position aesthetic mapped to the variable that has the counts.

Let’s now go back to the flights data frame in the nycflights13 package and visualize the distribution of the categorical variable carrier. In other words, let’s visualize the number of domestic flights out New York City each airline company flew in 2013. Recall from Section 1.4.3 when you first explored the flights data frame you saw that each row corresponds to a flight. In other words the flights data frame is more like the fruits data frame than the fruits_counted data frame because the flights have not been pre-counted by carrier. Thus we should use geom_bar() instead of geom_col() to create a barplot. Much like a geom_histogram(), there is only one variable in the aes() aesthetic mapping: the variable carrier gets mapped to the x-position.

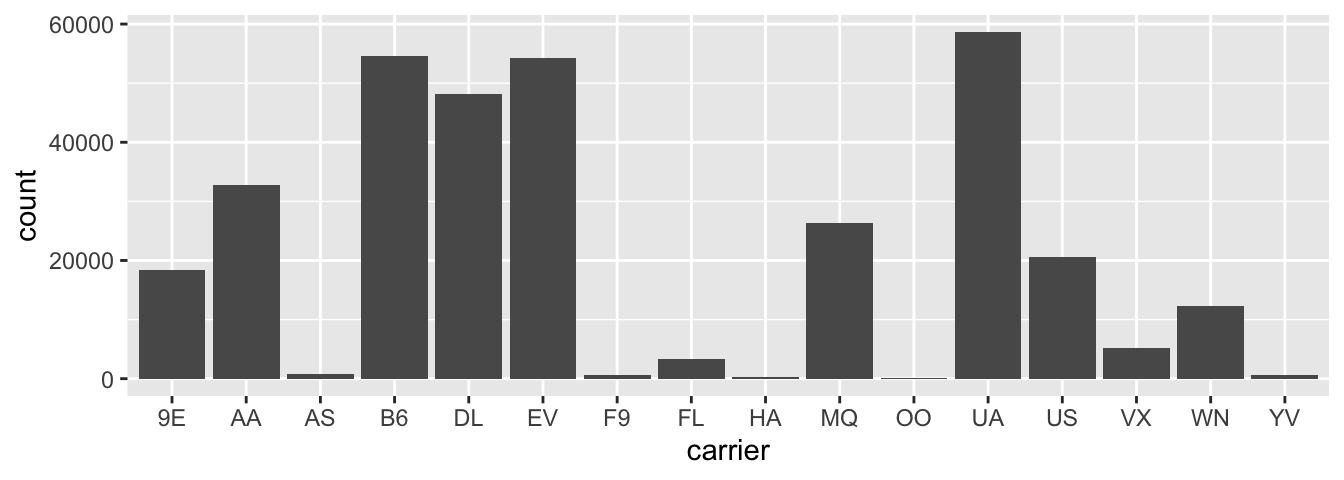
Number of flights departing NYC in 2013 by airline using geom_bar().

FIGURE 2.21: Number of flights departing NYC in 2013 by airline using geom_bar().

Observe in Figure 2.21 that United Air Lines (UA), JetBlue Airways (B6), and ExpressJet Airlines (EV) had the most flights depart New York City in 2013. If you don’t know which airlines correspond to which carrier codes, then run View(airlines) to see a directory of airlines. For example: AA is American Airlines; B6 is JetBlue Airways; DL is Delta Airlines; EV is ExpressJet Airlines; MQ is Envoy Air; while UA is United Airlines.

Alternatively, say you had a data frame flights_counted where the number of flights for each carrier was pre-counted like in Table 2.3.

TABLE 2.3: Number of flights pre-counted for each carrier.
carrier number
9E 18460
AA 32729
AS 714
B6 54635
DL 48110
EV 54173
F9 685
FL 3260
HA 342
MQ 26397
OO 32
UA 58665
US 20536
VX 5162
WN 12275
YV 601

In order to create a barplot visualizing the distribution of the categorical variable carrier in this case, we would use geom_col() instead with x mapped to carrier and y mapped to number as shown in what follows. The resulting barplot would be identical to Figure 2.21.

Learning check

(LC2.26) Why are histograms inappropriate for visualizing categorical variables?

(LC2.27) What is the difference between histograms and barplots?

(LC2.28) How many Envoy Air flights departed NYC in 2013?

(LC2.29) What was the seventh highest airline in terms of departed flights from NYC in 2013? How could we better present the table to get this answer quickly?

2.8.2 Must avoid pie charts!

One of the most common plots used to visualize the distribution of categorical data is the pie chart. While they may seem harmless enough, they actually present a problem in that humans are unable to judge angles well. As Naomi Robbins describes in her book “Creating More Effective Graphs” (Robbins 2013), we overestimate angles greater than 90 degrees and we underestimate angles less than 90 degrees. In other words, it is difficult for us to determine the relative size of one piece of the pie compared to another.

Let’s examine the same data used in our previous barplot of the number of flights departing NYC by airline in Figure 2.21, but this time we will use a pie chart in Figure 2.22. Try to answer the following questions:

  • How much larger is the portion of the pie for ExpressJet Airlines (EV) compared to US Airways (US),
  • What is the third largest carrier in terms of departing flights, and
  • How many carriers have fewer flights than United Airlines (UA)?
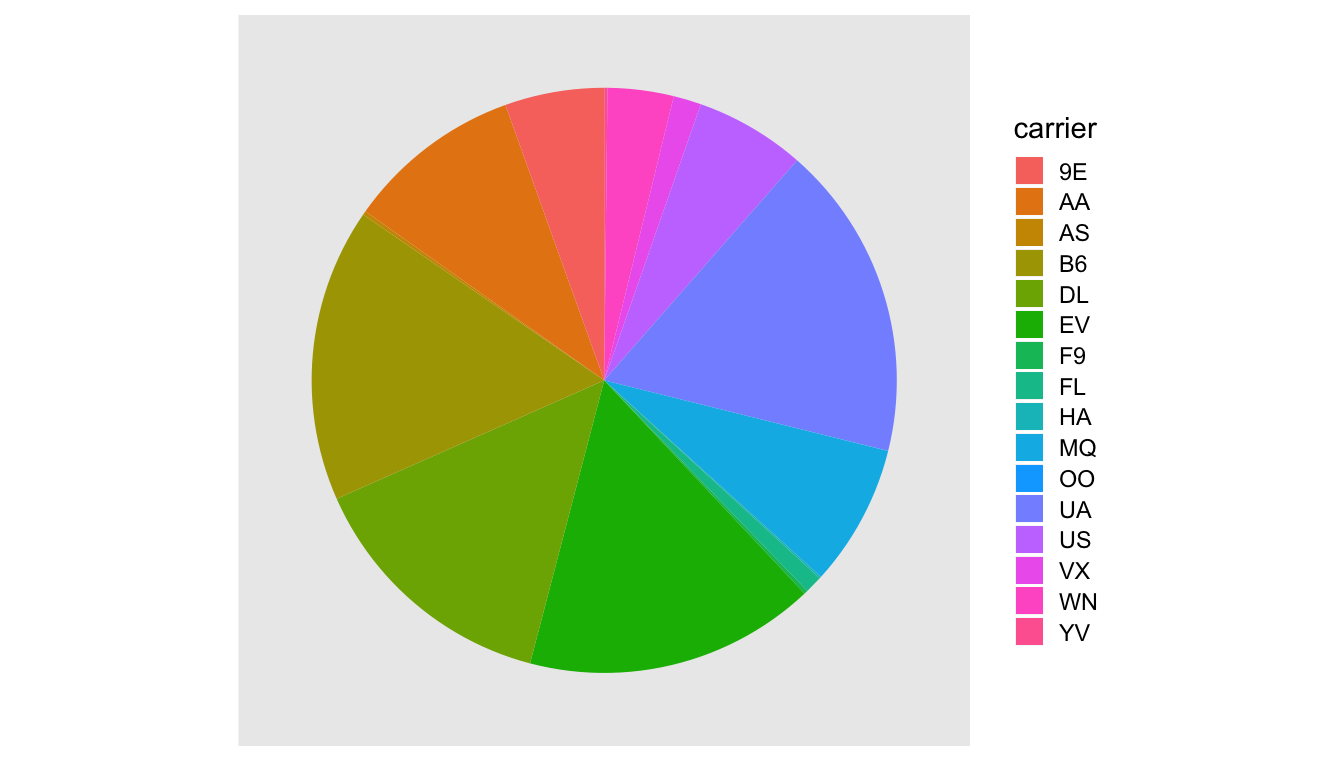
The dreaded pie chart.

FIGURE 2.22: The dreaded pie chart.

While it is quite difficult to answer these questions when looking at the pie chart in Figure 2.22, we can much more easily answer these questions using the barchart in Figure 2.21. This is true since barplots present the information in a way such that comparisons between categories can be made with single horizontal lines, whereas pie charts present the information in a way such that comparisons must be made by comparing angles.

Learning check

(LC2.30) Why should pie charts be avoided and replaced by barplots?

(LC2.31) Why do you think people continue to use pie charts?

2.8.3 Two categorical variables

Barplots are a very common way to visualize the frequency of different categories, or levels, of a single categorical variable. Another use of barplots is to visualize the joint distribution of two categorical variables at the same time. Let’s examine the joint distribution of outgoing domestic flights from NYC by carrier as well as origin. In other words, the number of flights for each carrier and origin combination. For example, the number of WestJet flights from JFK, the number of WestJet flights from LGA, the number of WestJet flights from EWR, the number of American Airlines flights from JFK, and so on. Recall the ggplot() code that created the barplot of carrier frequency in Figure 2.21:

We can now map the additional variable origin by adding a fill = origin inside the aes() aesthetic mapping; the fill aesthetic of any bar corresponds to the color used to fill the bars.

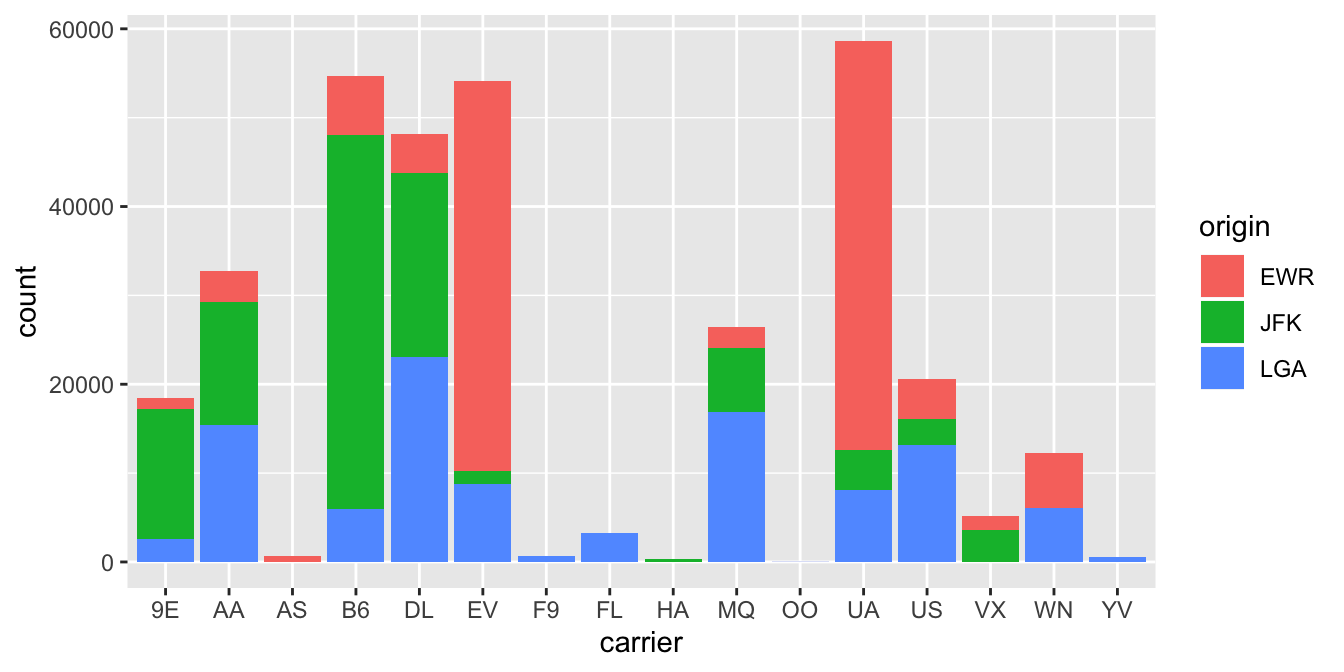
Stacked barplot comparing the number of flights by carrier and origin.

FIGURE 2.23: Stacked barplot comparing the number of flights by carrier and origin.

Figure 2.23 is an example of a stacked barplot. While simple to make, in certain aspects it is not ideal. For example, it is difficult to compare the heights of the different colors between the bars, corresponding to comparing the number of flights from each origin airport between the carriers.

Before we continue, let’s address some common points of confusion among new R users. First, note that fill is another aesthetic mapping much like x-position; thus we were careful to include it within the parentheses of the aes() mapping. The following code, where the fill aesthetic is specified outside the aes() mapping will yield an error. This is a fairly common error that new ggplot users make:

Second, the fill aesthetic corresponds to the color used to fill the bars, while the color aesthetic corresponds to the color of the outline of the bars. This is identical to how we added color to our histogram in Subsection 2.5.1: we set the outline of the bars to white by setting color = "white" and the colors of the bars to be blue steel by setting fill = "steelblue". Observe in Figure 2.24 that mapping origin to color and not fill yields grey bars with different colored outlines.

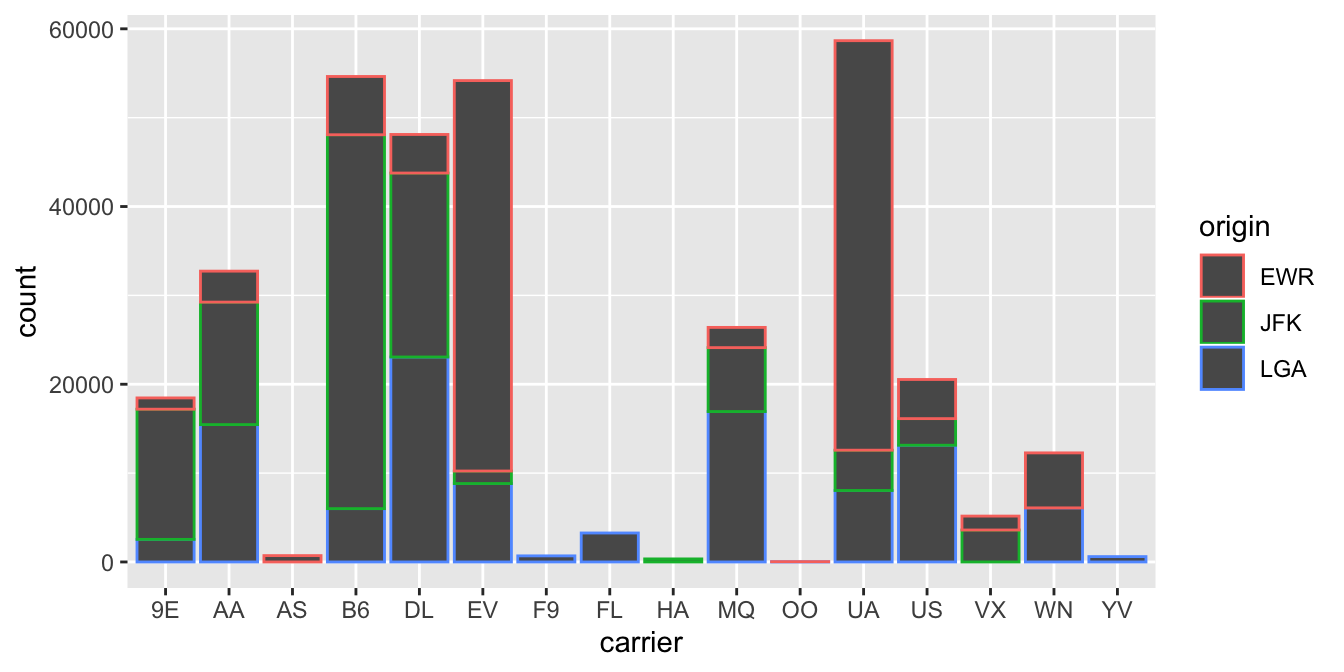
Stacked barplot with color aesthetic used instead of fill.

FIGURE 2.24: Stacked barplot with color aesthetic used instead of fill.

An alternative to stacked barplots are side-by-side barplots, also known as dodged barplots, as seen in Figure 2.25. The code to create a side-by-side barplot is identical to the code to create a stacked barplot, but with a position = "dodge" argument added to geom_bar(). In other words, we are overriding the default barplot type, which is a stacked barplot, and specifying it to be a side-by-side barplot.

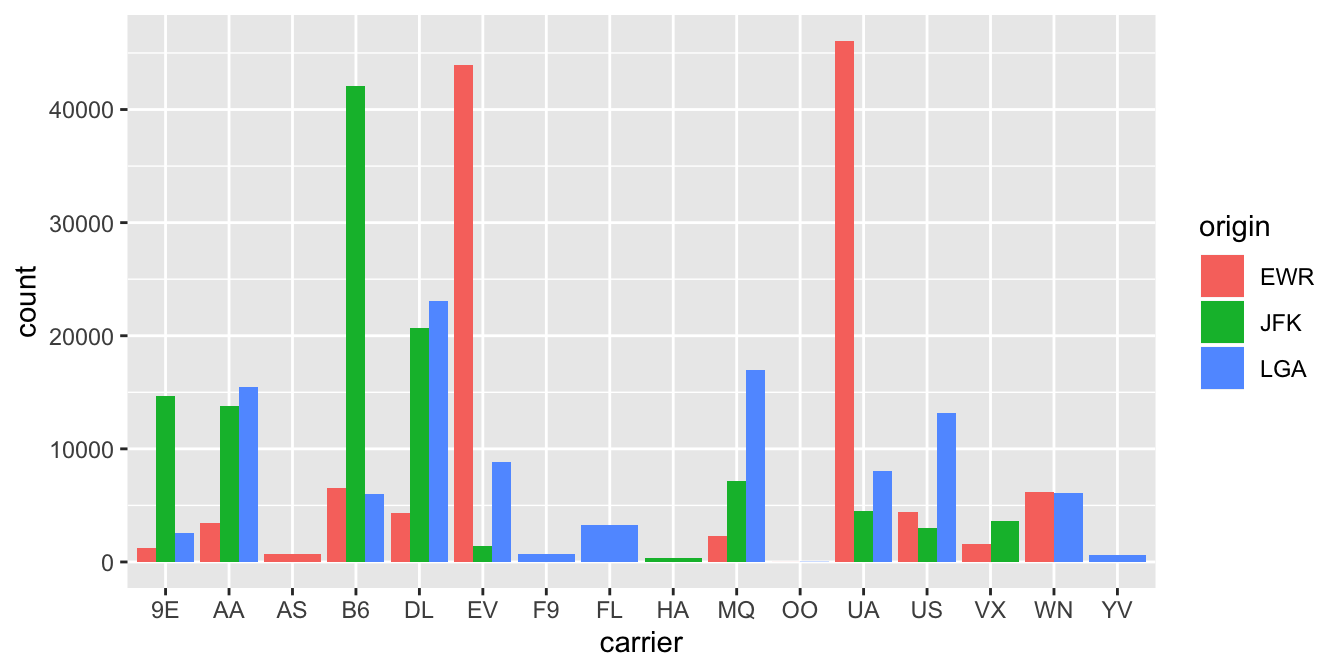
Side-by-side barplot comparing number of flights by carrier and origin.

FIGURE 2.25: Side-by-side barplot comparing number of flights by carrier and origin.

Lastly, another type of barplot is a faceted barplot. Recall in Section 2.6 we visualized the distribution of hourly temperatures at the 3 NYC airports split by month using facets. We apply the same principle to our barplot visualizing the frequency of carrier split by origin: instead of mapping origin

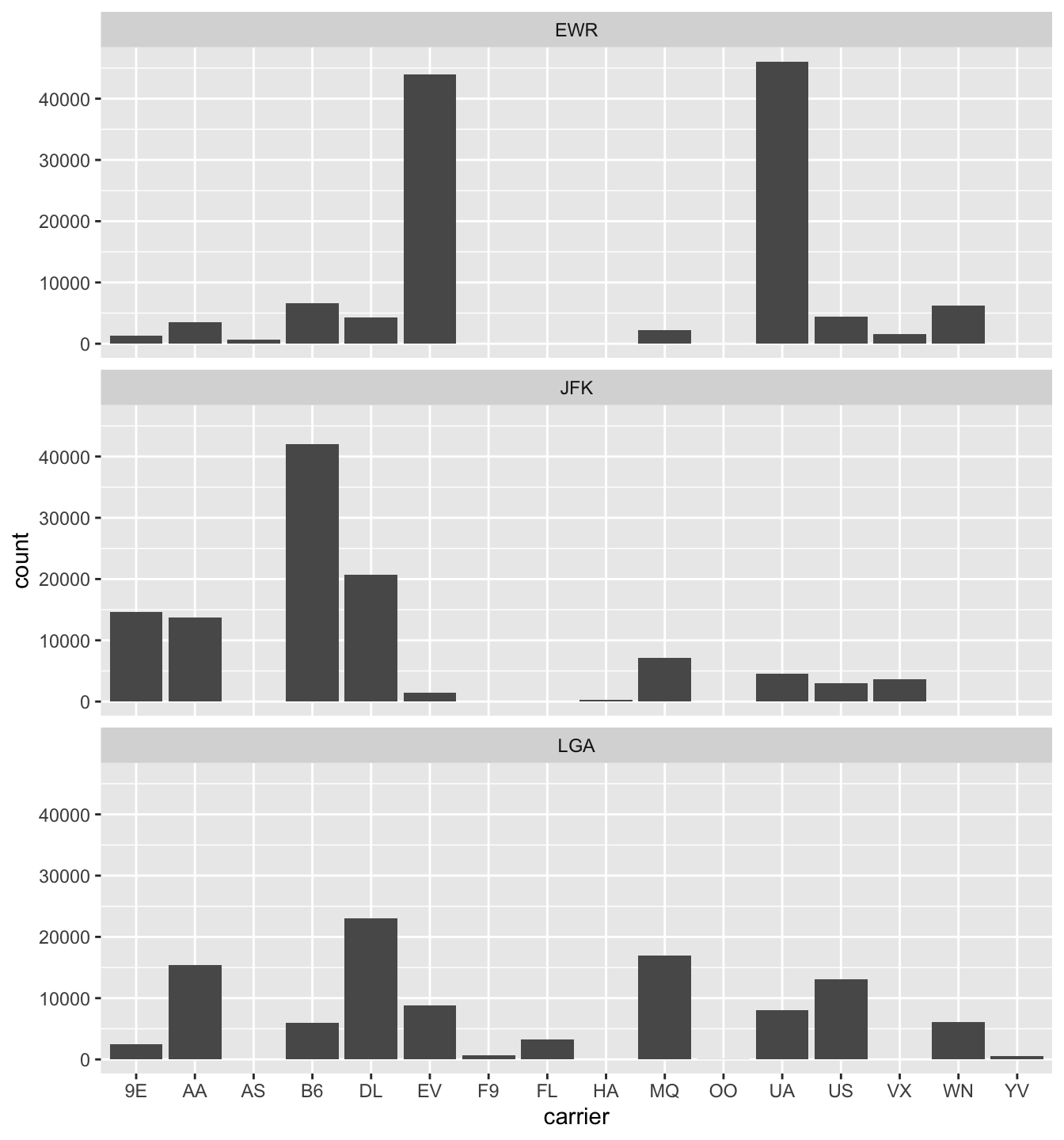
Faceted barplot comparing the number of flights by carrier and origin.

FIGURE 2.26: Faceted barplot comparing the number of flights by carrier and origin.

Learning check

(LC2.32) What kinds of questions are not easily answered by looking at Figure 2.23?

(LC2.33) What can you say, if anything, about the relationship between airline and airport in NYC in 2013 in regards to the number of departing flights?

(LC2.34) Why might the side-by-side (AKA dodged) barplot be preferable to a stacked barplot in this case?

(LC2.35) What are the disadvantages of using a side-by-side (AKA dodged) barplot, in general?

(LC2.36) Why is the faceted barplot preferred to the side-by-side and stacked barplots in this case?

(LC2.37) What information about the different carriers at different airports is more easily seen in the faceted barplot?

2.8.4 Summary

Barplots are a very common way of displaying the distribution of a categorical variable, or in other words the frequency with which the different categories (also called levels) occur. They are easy to understand and make it easy to make comparisons across levels. Furthermore, when trying to visualize the relationship of two categorical variables, you have many options: stacked barplots, side-by-side barplots, and faceted barplots. Depending on what aspect of the relationship you are trying to emphasize, you will need to make a choice between these three types of barplots and own that choice.

2.9 Conclusion

2.9.1 Summary table

Let’s recap all five of the Five Named Graphs (5NG) in Table 2.4 summarizing their differences. Using these 5NG, you’ll be able to visualize the distributions and relationships of variables contained in a wide array of datasets. This will be even more the case as we start to map more variables to more of each geometric object’s aesthetic attribute options, further unlocking the awesome power of the ggplot2 package.

TABLE 2.4: Summary of Five Named Graphs
Named graph Shows Geometric object Notes
1 Scatterplot Relationship between 2 numerical variables geom_point()
2 Linegraph Relationship between 2 numerical variables geom_line() Used when there is a sequential order to x-variable e.g. time
3 Histogram Distribution of 1 numerical variable geom_histogram() Facetted histograms show the distribution of 1 numerical variable split by the values of another variable
4 Boxplot Distribution of 1 numerical variable split by the values of another variable geom_boxplot()
5 Barplot Distribution of 1 categorical variable geom_bar() when counts are not pre-counted, geom_col() when counts are pre-counted Stacked, side-by-side, and faceted barplots show the joint distribution of 2 categorical variables

2.9.2 Function argument specification

Let’s go over some important points about specifying the arguments (i.e. inputs) to functions. Run the following two segments of code:

You’ll notice that that both code segments create the same barplot, even though in the second segment we omitted the data = and mapping = code argument names. This is because the ggplot() function by default assumes that the data argument comes first and the mapping argument comes second. So as long as you specify the data frame in question first and the aes() mapping second, you can omit the explicit statement of the argument names data = and mapping =.

Going forward for the rest of this book, all ggplot() code will be like the second segment: with the data = and mapping = explicit naming of the argument omitted with the default ordering of arguments respected. We’ll do this for brevity’s sake and it’s common to see this style when reviewing the R code of other R users.

2.9.3 Additional resources

An R script file of all R code used in this chapter is available here.

If you want to further unlock the power of the ggplot2 package for data visualization, we suggest that you check out RStudio’s “Data Visualization with ggplot2” cheatsheet. This cheatsheet summarizes much more than what we’ve discussed in this chapter. In particular it presents many more than the 5 geometric objects we covered in this chapter while providing quick and easy to read visual descriptions. For all the geometric objects, it also lists all the possible aesthetic attributes one can tweak. You can access this cheatsheet by going to the RStudio Menu Bar -> Help -> Cheatsheets -> “Data Visualization with ggplot2.” You can see a preview in the figure below.

Data Visualization with ggplot2 cheatsheet.

FIGURE 2.27: Data Visualization with ggplot2 cheatsheet.

2.9.4 What’s to come

Recall in Figure 2.2 in Section 2.3 we visualized the relationship between departure delay and arrival delay for Alaska Airlines flights. This necessitated paring down the flights data frame to a new data frame alaska_flights consisting of only carrier == AS flights first:

Furthermore recall in Figure 2.7 in Section 2.4 we visualized hourly temperature recordings at Newark airport only for the first 15 days of January 2013. This necessitated paring down the weather data frame to a new data frame early_january_weather consisting of hourly temperature recordings only for origin == "EWR", month == 1, and day less than or equal to 15 first:

These two code segments were a preview of Chapter 3 on data wrangling using the dplyr package. Data wrangling is the process of transforming and modifying existing data with the intent of making it more appropriate for analysis purposes. For example, the two code segments used the filter() function to create new data frames (alaska_flights and early_january_weather) by choosing only a subset of rows of existing data frames (flights and weather). In the next chapter, we’ll formally introduce the filter() and other data wrangling functions as well as the pipe operator %>% which allows you to combine multiple data wrangling actions into a single sequential chain of actions. On to Chapter 3 on data wrangling!

References

Grolemund, Garrett, and Hadley Wickham. 2016. R for Data Science. http://r4ds.had.co.nz/.

Robbins, Naomi. 2013. Creating More Effective Graphs. Chart House.

Wickham, Hadley, Winston Chang, Lionel Henry, Thomas Lin Pedersen, Kohske Takahashi, Claus Wilke, Kara Woo, and Hiroaki Yutani. 2019. Ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics. https://CRAN.R-project.org/package=ggplot2.

Wilkinson, Leland. 2005. The Grammar of Graphics (Statistics and Computing). Secaucus, NJ, USA: Springer-Verlag New York, Inc.