Take a `moderndive` into introductory linear regression with R
Albert Y. Kim, Chester Ismay, and Max Kuhn
2025-11-18
Source:vignettes/paper.Rmd
paper.RmdSummary
We present the moderndive R package of datasets and
functions for tidyverse-friendly introductory
linear regression (Wickham, Averick, et al.
2019). These tools leverage the well-developed
tidyverse and broom packages to facilitate 1)
working with regression tables that include confidence intervals, 2)
accessing regression outputs on an observation level
(e.g. fitted/predicted values and residuals), 3) inspecting scalar
summaries of regression fit
(e.g. ,
,
and mean squared error), and 4) visualizing parallel slopes regression
models using ggplot2-like syntax (Wickham, Chang, et al. 2019; Robinson and Hayes
2019). This R package is designed to supplement the book
“Statistical Inference via Data Science: A ModernDive into R and the
Tidyverse” (Ismay and Kim 2019). Note that
the book is also available online at https://moderndive.com and is referred to as
“ModernDive” for short.
Statement of Need
Linear regression has long been a staple of introductory statistics
courses. While the curricula of introductory statistics courses has much
evolved of late, the overall importance of regression remains the same
(American Statistical Association Undergraduate
Guidelines Workgroup 2016). Furthermore, while the use of the R
statistical programming language for statistical analysis is not new,
recent developments such as the tidyverse suite of packages
have made statistical computation with R accessible to a broader
audience (Wickham, Averick, et al. 2019).
We go one step further by leveraging the tidyverse and the
broom packages to make linear regression accessible to
students taking an introductory statistics course (Robinson and Hayes 2019). Such students are
likely to be new to statistical computation with R; we designed
moderndive with these students in mind.
Introduction
Let’s load all the R packages we are going to need.
Let’s consider data gathered from end of semester student evaluations
for a sample of 463 courses taught by 94 professors from the University
of Texas at Austin (Diez, Barr, and
Çetinkaya-Rundel 2015). This data is included in the
evals data frame from the moderndive
package.
In the following table, we present a subset of 9 of the 14 variables included for a random sample of 5 courses1:
-
IDuniquely identifies the course whereasprof_IDidentifies the professor who taught this course. This distinction is important since many professors taught more than one course. -
scoreis the outcome variable of interest: average professor evaluation score out of 5 as given by the students in this course. - The remaining variables are demographic variables describing that
course’s instructor, including
bty_avg(average “beauty” score) for that professor as given by a panel of 6 students.2
| ID | prof_ID | score | age | bty_avg | gender | ethnicity | language | rank |
|---|---|---|---|---|---|---|---|---|
| 129 | 23 | 3.7 | 62 | 3.000 | male | not minority | english | tenured |
| 109 | 19 | 4.7 | 46 | 4.333 | female | not minority | english | tenured |
| 28 | 6 | 4.8 | 62 | 5.500 | male | not minority | english | tenured |
| 434 | 88 | 2.8 | 62 | 2.000 | male | not minority | english | tenured |
| 330 | 66 | 4.0 | 64 | 2.333 | male | not minority | english | tenured |
Regression analysis the “good old-fashioned” way
Let’s fit a simple linear regression model of teaching
score as a function of instructor age using
the lm() function.
score_model <- lm(score ~ age, data = evals)Let’s now study the output of the fitted model
score_model “the good old-fashioned way”: using
summary() which calls summary.lm() behind the
scenes (we’ll refer to them interchangeably throughout this paper).
summary(score_model)
##
## Call:
## lm(formula = score ~ age, data = evals)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.9185 -0.3531 0.1172 0.4172 0.8825
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.461932 0.126778 35.195 <2e-16 ***
## age -0.005938 0.002569 -2.311 0.0213 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5413 on 461 degrees of freedom
## Multiple R-squared: 0.01146, Adjusted R-squared: 0.009311
## F-statistic: 5.342 on 1 and 461 DF, p-value: 0.02125Regression analysis using moderndive
As an improvement to base R’s regression functions, we’ve included
three functions in the moderndive package that take a
fitted model object as input and return the same information as
summary.lm(), but output them in tidyverse-friendly format
(Wickham, Averick, et al. 2019). As we’ll
see later, while these three functions are thin wrappers to existing
functions in the broom package for converting statistical
objects into tidy tibbles, we modified them with the introductory
statistics student in mind (Robinson and Hayes
2019).
-
Get a tidy regression table with confidence intervals:
get_regression_table(score_model) ## # A tibble: 2 × 7 ## term estimate std_error statistic p_value lower_ci upper_ci ## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 intercept 4.46 0.127 35.2 0 4.21 4.71 ## 2 age -0.006 0.003 -2.31 0.021 -0.011 -0.001 -
Get information on each point/observation in your regression, including fitted/predicted values and residuals, in a single data frame:
get_regression_points(score_model) ## # A tibble: 463 × 5 ## ID score age score_hat residual ## <int> <dbl> <int> <dbl> <dbl> ## 1 1 4.7 36 4.25 0.452 ## 2 2 4.1 36 4.25 -0.148 ## 3 3 3.9 36 4.25 -0.348 ## 4 4 4.8 36 4.25 0.552 ## 5 5 4.6 59 4.11 0.488 ## 6 6 4.3 59 4.11 0.188 ## 7 7 2.8 59 4.11 -1.31 ## 8 8 4.1 51 4.16 -0.059 ## 9 9 3.4 51 4.16 -0.759 ## 10 10 4.5 40 4.22 0.276 ## # ℹ 453 more rows -
Get scalar summaries of a regression fit including and but also the (root) mean-squared error:
get_regression_summaries(score_model) ## # A tibble: 1 × 9 ## r_squared adj_r_squared mse rmse sigma statistic p_value df ## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 0.011 0.009 0.292 0.540 0.541 5.34 0.021 1 ## # ℹ 1 more variable: nobs <dbl>
Furthermore, say you would like to create a visualization of the
relationship between two numerical variables and a third categorical
variable with
levels. Let’s create this using a colored scatterplot via the
ggplot2 package for data visualization (Wickham, Chang, et al. 2019). Using
geom_smooth(method = "lm", se = FALSE) yields a
visualization of an interaction model where each of the
regression lines has their own intercept and slope. For example in , we
extend our previous regression model by now mapping the categorical
variable ethnicity to the color aesthetic.
# Code to visualize interaction model:
ggplot(evals, aes(x = age, y = score, color = ethnicity)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE) +
labs(x = "Age", y = "Teaching score", color = "Ethnicity")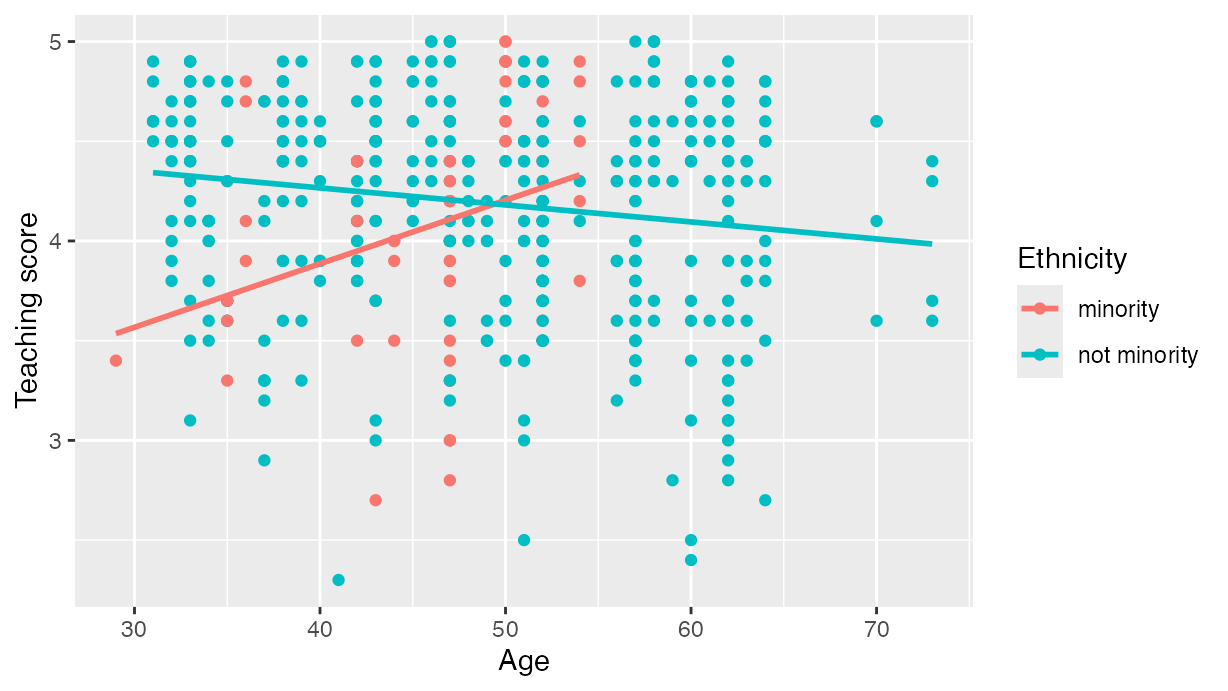
Visualization of interaction model.
However, many introductory statistics courses start with the easier
to teach “common slope, different intercepts” regression model, also
known as the parallel slopes model. However, no argument to
plot such models exists within geom_smooth().
Evgeni
Chasnovski thus wrote a custom geom_ extension to
ggplot2 called geom_parallel_slopes(); this
extension is included in the moderndive package. Much like
geom_smooth() from the ggplot2 package, you
add geom_parallel_slopes() as a layer to the code,
resulting in .
# Code to visualize parallel slopes model:
ggplot(evals, aes(x = age, y = score, color = ethnicity)) +
geom_point() +
geom_parallel_slopes(se = FALSE) +
labs(x = "Age", y = "Teaching score", color = "Ethnicity")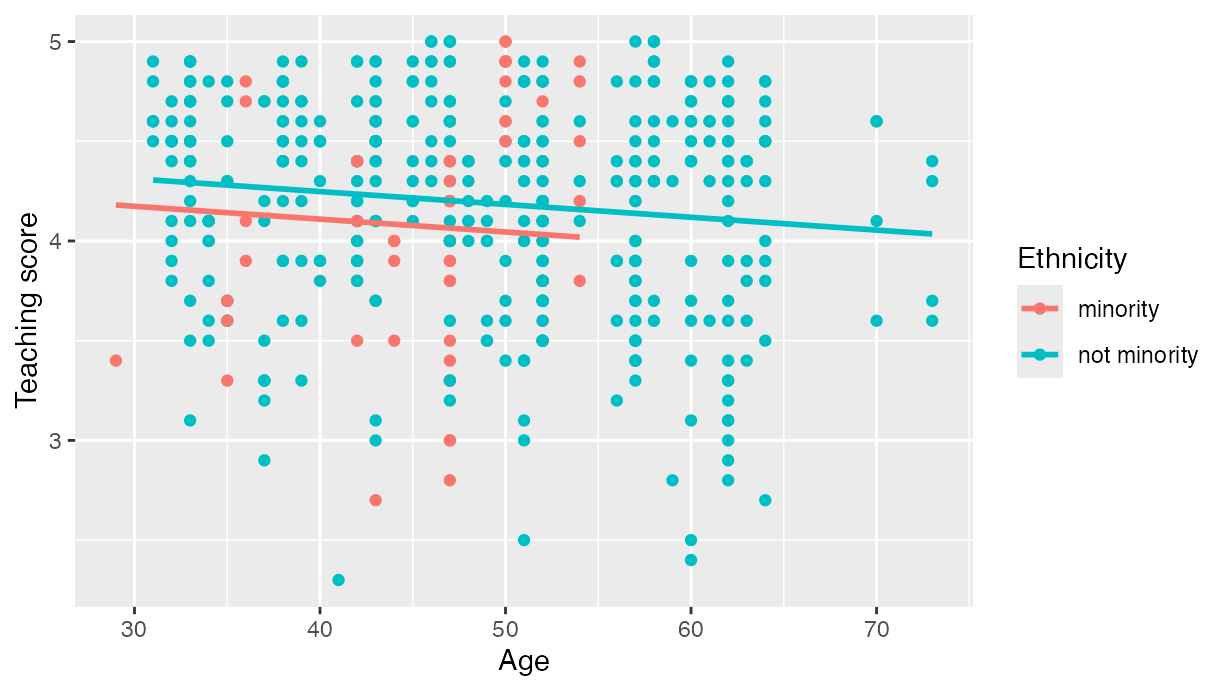
Visualization of parallel slopes model.
Repository README
In the GitHub repository README, we present an in-depth discussion of
six features of the moderndive package:
- Focus less on p-value stars, more confidence intervals
- Outputs as tibbles
- Produce residual analysis plots from scratch using
ggplot2 - A quick-and-easy Kaggle predictive modeling competition submission!
- Visual model selection: plot parallel slopes & interaction regression models
- Produce metrics on the quality of regression model fits
Furthermore, we discuss the inner-workings of the
moderndive package:
- It leverages the
broompackage in its wrappers - It builds a custom
ggplot2geometry for thegeom_parallel_slopes()function that allows for quick visualization of parallel slopes models in regression.
Author contributions
Albert Y. Kim and Chester Ismay contributed equally to the
development of the moderndive package. Albert Y. Kim wrote
a majority of the initial version of this manuscript with Chester Ismay
writing the rest. Max Kuhn provided guidance and feedback at various
stages of the package development and manuscript writing.
Acknowledgments
Many thanks to Jenny Smetzer @smetzer180, Luke W. Johnston @lwjohnst86,
and Lisa Rosenthal @lisamr for their helpful feedback for this paper
and to Evgeni Chasnovski @echasnovski for contributing the
geom_parallel_slopes() function via GitHub pull request. The authors do not have any financial
support to disclose.