ModernDive

Chapter 3 Data Wrangling

So far in our journey, we’ve seen how to look at data saved in data frames using the glimpse() and View() functions in Chapter 1, and how to create data visualizations using the ggplot2 package in Chapter 2. In particular we studied what we term the “five named graphs” (5NG):

  1. scatterplots via geom_point()
  2. linegraphs via geom_line()
  3. boxplots via geom_boxplot()
  4. histograms via geom_histogram()
  5. barplots via geom_bar() or geom_col()

We created these visualizations using the grammar of graphics, which maps variables in a data frame to the aesthetic attributes of one of the 5 geometric objects. We can also control other aesthetic attributes of the geometric objects such as the size and color as seen in the Gapminder data example in Figure 2.1.

Recall however that for two of our visualizations, we first needed to transform/modify existing data frames a little. For example, recall the scatterplot in Figure 2.2 of departure and arrival delays only for Alaska Airlines flights. In order to create this visualization, we first needed to pare down the flights data frame to an alaska_flights data frame consisting of only carrier == "AS" flights. Thus, alaska_flights will have fewer rows than flights. We did this using the filter() function:

In this chapter, we’ll extend this example and we’ll introduce a series of functions from the dplyr package for data wrangling that will allow you to take a data frame and “wrangle” it (transform it) to suit your needs. Such functions include:

  1. filter() a data frame’s existing rows to only pick out a subset of them. For example, the alaska_flights data frame.
  2. summarize() one or more of its columns/variables with a summary statistic. Examples of summary statistics include the median and interquartile range of temperatures as we saw in Section 2.7 on boxplots.
  3. group_by() its rows. In other words, assign different rows to be part of the same group. We can then combine group_by() with summarize() to report summary statistics for each group separately. For example, say you don’t want a single overall average departure delay dep_delay for all three origin airports combined, but rather three separate average departure delays, one computed for each of the three origin airports.
  4. mutate() its existing columns/variables to create new ones. For example, convert hourly temperature recordings from degrees Fahrenheit to degrees Celsius.
  5. arrange() its rows. For example, sort the rows of weather in ascending or descending order of temp.
  6. join() it with another data frame by matching along a “key” variable. In other words, merge these two data frames together.

Notice how we used computer_code font to describe the actions we want to take on our data frames. This is because the dplyr package for data wrangling has intuitively verb-named functions that are easy to remember.

There is a further benefit to learning to use the dplyr package for data wrangling: its similarity to the database querying language SQL (pronounced “sequel” or spelled out as “S”, “Q”, “L”). SQL (which stands for “Structured Query Language”) is used to manage large databases quickly and efficiently and is widely used by many institutions with a lot of data. While SQL is a topic left for a book or a course on database management, keep in mind that once you learn dplyr, you can learn SQL easily. We’ll talk more about their similarities in Subsection 3.7.4.

Needed packages

Let’s load all the packages needed for this chapter (this assumes you’ve already installed them). If needed, read Section 1.3 for information on how to install and load R packages.

3.1 The pipe operator: %>%

Before we start data wrangling, let’s first introduce a nifty tool that gets loaded with the dplyr package: the pipe operator %>%. The pipe operator allows us to combine multiple operations in R into a single sequential chain of actions.

Let’s start with a hypothetical example. Say you would like to perform a hypothetical sequence of operations on a hypothetical data frame x using hypothetical functions f(), g(), and h():

  1. Take x then
  2. Use x as an input to a function f() then
  3. Use the output of f(x) as an input to a function g() then
  4. Use the output of g(f(x)) as an input to a function h()

One way to achieve this sequence of operations is by using nesting parentheses as follows:

This code isn’t so hard to read since we are applying only three functions: f(), then g(), then h() and each of the functions is short in its name. Further, each of these functions also only has one argument. However, you can imagine that this will get progressively harder to read as the number of functions applied in your sequence increases and the arguments in each function increase as well. This is where the pipe operator %>% comes in handy. %>% takes the output of one function and then “pipes” it to be the input of the next function. Furthermore, a helpful trick is to read %>% as “then” or “and then.” For example, you can obtain the same output as the hypothetical sequence of functions as follows:

You would read this sequence as:

  1. Take x then
  2. Use this output as the input to the next function f() then
  3. Use this output as the input to the next function g() then
  4. Use this output as the input to the next function h()

So while both approaches achieve the same goal, the latter is much more human-readable because you can clearly read the sequence of operations line-by-line. But what are the hypothetical x, f(), g(), and h()? Throughout this chapter on data wrangling:

  1. The starting value x will be a data frame. For example, the flights data frame we explored in Section 1.4.
  2. The sequence of functions, here f(), g(), and h(), will mostly be a sequence of any number of the six data wrangling verb-named functions we listed in the introduction to this chapter. For example, the filter(carrier == "AS") function and argument specified we previewed earlier.
  3. The result will be the transformed/modified data frame that you want. In our example, we’ll save the result in a new data frame by using the <- assignment operator with the name alaska_flights via alaska_flights <-.

Much like when adding layers to a ggplot() using the + sign, you form a single chain of data wrangling operations by combining verb-named functions into a single sequence using the pipe operator %>%. Furthermore, much like how the + sign has to come at the end of lines when constructing plots, the pipe operator %>% has to come at the end of lines as well.

Keep in mind, there are many more advanced data wrangling functions than just the six listed in the introduction to this chapter; you’ll see some examples of these in Section 3.8. However, just with these six verb-named functions you’ll be able to perform a broad array of data wrangling tasks for the rest of this book.

3.2 filter rows

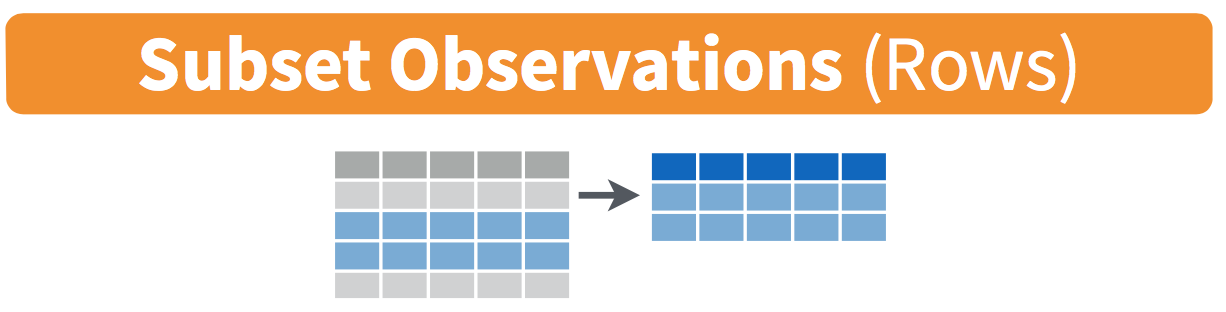
Diagram of filter() rows operation.

FIGURE 3.1: Diagram of filter() rows operation.

The filter() function here works much like the “Filter” option in Microsoft Excel; it allows you to specify criteria about the values of a variable in your dataset and then filters out only the rows that match that criteria.

We begin by focusing only on flights from New York City to Portland, Oregon. The dest destination code (or airport code) for Portland, Oregon is "PDX". Run the following and look at the results in RStudio’s spreadsheet viewer to ensure that only flights heading to Portland are chosen here:

Note the order of the code. First, take the flights data frame flights then filter() the data frame so that only those where the dest equals "PDX" are included. We test for equality using the double equal sign == and not a single equal sign =. In other words filter(dest = "PDX") will yield an error. This is a convention across many programming languages. If you are new to coding, you’ll probably forget to use the double equal sign == a few times before you get the hang of it.

You can use other operators beyond just the == operator that tests for equality:

  • > corresponds to “greater than”
  • < corresponds to “less than”
  • >= corresponds to “greater than or equal to”
  • <= corresponds to “less than or equal to”
  • != corresponds to “not equal to.” The ! is used in many programming languages to indicate “not.”

Furthermore, you can combine multiple criteria using operators that make comparisons:

  • | corresponds to “or”
  • & corresponds to “and”

To see many of these in action, let’s filter flights for all rows that departed from JFK and were heading to Burlington, Vermont ("BTV") or Seattle, Washington ("SEA") and departed in the months of October, November, or December. Run the following:

Note that even though colloquially speaking one might say “all flights leaving Burlington, Vermont and Seattle, Washington,” in terms of computer operations, we really mean “all flights leaving Burlington, Vermont or leaving Seattle, Washington.” For a given row in the data, dest can be "BTV", or "SEA", or something else, but not both "BTV" and "SEA" at the same time. Furthermore, note the careful use of parentheses around dest == "BTV" | dest == "SEA".

We can often skip the use of & and just separate our conditions with a comma. The previous code will return the identical output btv_sea_flights_fall as the following code:

Let’s present another example that uses the ! “not” operator to pick rows that don’t match a criteria. As mentioned earlier, the ! can be read as “not.” Here we are filtering rows corresponding to flights that didn’t go to Burlington, VT or Seattle, WA.

Again, note the careful use of parentheses around the (dest == "BTV" | dest == "SEA"). If we didn’t use parentheses as follows:

We would be returning all flights not headed to "BTV" or those headed to "SEA", which is an entirely different resulting data frame.

Now say we have a larger number of airports we want to filter for, say "SEA", "SFO", "PDX", "BTV", and "BDL". We could continue to use the | (or) operator:

but as we progressively include more airports, this will get unwieldy to write. A slightly shorter approach uses the %in% operator along with the c() function. Recall from Subsection 1.2.1 that the c() function “combines” or “concatenates” values into a single vector of values.

What this code is doing is filtering flights for all flights where dest is in the vector of airports c("BTV", "SEA", "PDX", "SFO", "BDL"). Both outputs of many_airports are the same, but as you can see the latter takes much less energy to code. The %in% operator is useful for looking for matches commonly in one vector/variable compared to another.

As a final note, we recommend that filter() should often be among the first verbs you consider applying to your data. This cleans your dataset to only those rows you care about, or put differently, it narrows down the scope of your data frame to just the observations you care about.

Learning check

(LC3.1) What’s another way of using the “not” operator ! to filter only the rows that are not going to Burlington, VT nor Seattle, WA in the flights data frame? Test this out using the previous code.

3.3 summarize variables

The next common task when working with data frames is to compute summary statistics. Summary statistics are single numerical values that summarize a large number of values. Commonly known examples of summary statistics include the mean (also called the average) and the median (the middle value). Other examples of summary statistics that might not immediately come to mind include the sum, the smallest value also called the minimum, the largest value also called the maximum, and the standard deviation. See Appendix A.1 for a glossary of such summary statistics.

Let’s calculate two summary statistics of the temp temperature variable in the weather data frame: the mean and standard deviation (recall from Section 1.4 that the weather data frame is included in the nycflights13 package). To compute these summary statistics, we need the mean() and sd() summary functions in R. Summary functions in R take in many values and return a single value, as illustrated in Figure 3.2.

Diagram illustrating a summary function in R.

FIGURE 3.2: Diagram illustrating a summary function in R.

More precisely, we’ll use the mean() and sd() summary functions within the summarize() function from the dplyr package. Note you can also use the British English spelling of summarise(). As shown in Figure 3.3, the summarize() function takes in a data frame and returns a data frame with only one row corresponding to the summary statistics.

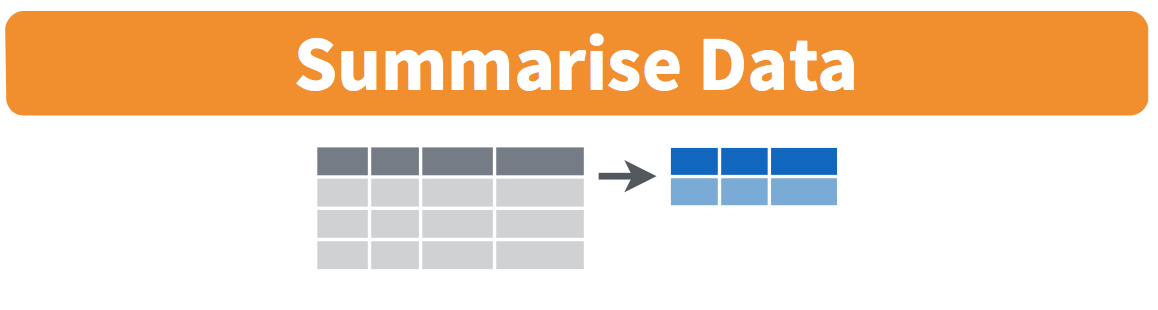
Diagram of summarize() rows.

FIGURE 3.3: Diagram of summarize() rows.

We’ll save the results in a new data frame called summary_temp that will have two columns/variables: the mean and the std_dev:

# A tibble: 1 x 2
   mean std_dev
  <dbl>   <dbl>
1    NA      NA

Why are the values returned NA? As we saw in Subsection 2.3.1 when creating the scatterplot of departure and arrival delays for alaska_flights, NA is how R encodes missing values where NA indicates “not available” or “not applicable.” If a value for a particular row and a particular column does not exist, NA is stored instead. Values can be missing for many reasons. Perhaps the data was collected but someone forgot to enter it? Perhaps the data was not collected at all because it was too difficult to do so? Perhaps there was an erroneous value that someone entered that has been corrected to read as missing? You’ll often encounter issues with missing values when working with real data.

Going back to our summary_temp output, by default any time you try to calculate a summary statistic of a variable that has one or more NA missing values in R, NA is returned. To work around this fact, you can set the na.rm argument to TRUE, where rm is short for “remove”; this will ignore any NA missing values and only return the summary value for all non-missing values.

The code that follows computes the mean and standard deviation of all non-missing values of temp:

# A tibble: 1 x 2
   mean std_dev
  <dbl>   <dbl>
1  55.3    17.8

Notice how the na.rm = TRUE are used as arguments to the mean() and sd() summary functions individually, and not to the summarize() function.

However, one needs to be cautious whenever ignoring missing values as we’ve just done. In the upcoming Learning checks questions, we’ll consider the possible ramifications of blindly sweeping rows with missing values “under the rug.” This is in fact why the na.rm argument to any summary statistic function in R is set to FALSE by default. In other words, R does not ignore rows with missing values by default. R is alerting you to the presence of missing data and you should be mindful of this missingness and any potential causes of this missingness throughout your analysis.

What are other summary functions we can use inside the summarize() verb to compute summary statistics? As seen in the diagram in Figure 3.2, you can use any function in R that takes many values and returns just one. Here are just a few:

  • mean(): the average
  • sd(): the standard deviation, which is a measure of spread
  • min() and max(): the minimum and maximum values, respectively
  • IQR(): interquartile range
  • sum(): the total amount when adding multiple numbers
  • n(): a count of the number of rows in each group. This particular summary function will make more sense when group_by() is covered in Section 3.4.

Learning check

(LC3.2) Say a doctor is studying the effect of smoking on lung cancer for a large number of patients who have records measured at five-year intervals. She notices that a large number of patients have missing data points because the patient has died, so she chooses to ignore these patients in her analysis. What is wrong with this doctor’s approach?

(LC3.3) Modify the summarize() function to create summary_temp to also use the n() summary function: summarize(count = n()). What does the returned value correspond to?

(LC3.4) Why doesn’t the following code work? Run the code line-by-line instead of all at once, and then look at the data. In other words, run summary_temp <- weather %>% summarize(mean = mean(temp, na.rm = TRUE)) first.

3.4 group_by rows

Diagram of group_by() and summarize().

FIGURE 3.4: Diagram of group_by() and summarize().

Say instead of a single mean temperature for the whole year, you would like 12 mean temperatures, one for each of the 12 months separately. In other words, we would like to compute the mean temperature split by month. We can do this by “grouping” temperature observations by the values of another variable, in this case by the 12 values of the variable month. Run the following code:

# A tibble: 12 x 3
   month  mean std_dev
   <int> <dbl>   <dbl>
 1     1  35.6   10.2 
 2     2  34.3    6.98
 3     3  39.9    6.25
 4     4  51.7    8.79
 5     5  61.8    9.68
 6     6  72.2    7.55
 7     7  80.1    7.12
 8     8  74.5    5.19
 9     9  67.4    8.47
10    10  60.1    8.85
11    11  45.0   10.4 
12    12  38.4    9.98

This code is identical to the previous code that created summary_temp, but with an extra group_by(month) added before the summarize(). Grouping the weather dataset by month and then applying the summarize() functions yields a data frame that displays the mean and standard deviation temperature split by the 12 months of the year.

It is important to note that the group_by() function doesn’t change data frames by itself. Rather it changes the meta-data, or data about the data, specifically the grouping structure. It is only after we apply the summarize() function that the data frame changes.

For example, let’s consider the diamonds data frame included in the ggplot2 package. Run this code:

# A tibble: 53,940 x 10
   carat cut       color clarity depth table price     x     y     z
   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
 1 0.23  Ideal     E     SI2      61.5    55   326  3.95  3.98  2.43
 2 0.21  Premium   E     SI1      59.8    61   326  3.89  3.84  2.31
 3 0.23  Good      E     VS1      56.9    65   327  4.05  4.07  2.31
 4 0.290 Premium   I     VS2      62.4    58   334  4.2   4.23  2.63
 5 0.31  Good      J     SI2      63.3    58   335  4.34  4.35  2.75
 6 0.24  Very Good J     VVS2     62.8    57   336  3.94  3.96  2.48
 7 0.24  Very Good I     VVS1     62.3    57   336  3.95  3.98  2.47
 8 0.26  Very Good H     SI1      61.9    55   337  4.07  4.11  2.53
 9 0.22  Fair      E     VS2      65.1    61   337  3.87  3.78  2.49
10 0.23  Very Good H     VS1      59.4    61   338  4     4.05  2.39
# … with 53,930 more rows

Observe that the first line of the output reads # A tibble: 53,940 x 10. This is an example of meta-data, in this case the number of observations/rows and variables/columns in diamonds. The actual data itself are the subsequent table of values. Now let’s pipe the diamonds data frame into group_by(cut):

# A tibble: 53,940 x 10
# Groups:   cut [5]
   carat cut       color clarity depth table price     x     y     z
   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
 1 0.23  Ideal     E     SI2      61.5    55   326  3.95  3.98  2.43
 2 0.21  Premium   E     SI1      59.8    61   326  3.89  3.84  2.31
 3 0.23  Good      E     VS1      56.9    65   327  4.05  4.07  2.31
 4 0.290 Premium   I     VS2      62.4    58   334  4.2   4.23  2.63
 5 0.31  Good      J     SI2      63.3    58   335  4.34  4.35  2.75
 6 0.24  Very Good J     VVS2     62.8    57   336  3.94  3.96  2.48
 7 0.24  Very Good I     VVS1     62.3    57   336  3.95  3.98  2.47
 8 0.26  Very Good H     SI1      61.9    55   337  4.07  4.11  2.53
 9 0.22  Fair      E     VS2      65.1    61   337  3.87  3.78  2.49
10 0.23  Very Good H     VS1      59.4    61   338  4     4.05  2.39
# … with 53,930 more rows

Observe that now there is additional meta-data: # Groups: cut [5] indicating that the grouping structure meta-data has been set based on the 5 possible levels of the categorical variable cut: "Fair", "Good", "Very Good", "Premium", and "Ideal". On the other hand, observe that the data has not changed: it is still a table of 53,940 \(\times\) 10 values.

Only by combining a group_by() with another data wrangling operation, in this case summarize(), will the data actually be transformed.

# A tibble: 5 x 2
  cut       avg_price
  <ord>         <dbl>
1 Fair          4359.
2 Good          3929.
3 Very Good     3982.
4 Premium       4584.
5 Ideal         3458.

If you would like to remove this grouping structure meta-data, we can pipe the resulting data frame into the ungroup() function:

# A tibble: 53,940 x 10
   carat cut       color clarity depth table price     x     y     z
   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
 1 0.23  Ideal     E     SI2      61.5    55   326  3.95  3.98  2.43
 2 0.21  Premium   E     SI1      59.8    61   326  3.89  3.84  2.31
 3 0.23  Good      E     VS1      56.9    65   327  4.05  4.07  2.31
 4 0.290 Premium   I     VS2      62.4    58   334  4.2   4.23  2.63
 5 0.31  Good      J     SI2      63.3    58   335  4.34  4.35  2.75
 6 0.24  Very Good J     VVS2     62.8    57   336  3.94  3.96  2.48
 7 0.24  Very Good I     VVS1     62.3    57   336  3.95  3.98  2.47
 8 0.26  Very Good H     SI1      61.9    55   337  4.07  4.11  2.53
 9 0.22  Fair      E     VS2      65.1    61   337  3.87  3.78  2.49
10 0.23  Very Good H     VS1      59.4    61   338  4     4.05  2.39
# … with 53,930 more rows

Observe how the # Groups: cut [5] meta-data is no longer present.

Let’s now revisit the n() counting summary function we briefly introduced previously. Recall that the n() function counts rows. This is opposed to the sum() summary function that returns the sum of a numerical variable. For example, suppose we’d like to count how many flights departed each of the three airports in New York City:

# A tibble: 3 x 2
  origin  count
  <chr>   <int>
1 EWR    120835
2 JFK    111279
3 LGA    104662

We see that Newark ("EWR") had the most flights departing in 2013 followed by "JFK" and lastly by LaGuardia ("LGA"). Note there is a subtle but important difference between sum() and n(); while sum() returns the sum of a numerical variable, n() returns a count of the number of rows/observations.

3.4.1 Grouping by more than one variable

You are not limited to grouping by one variable. Say you want to know the number of flights leaving each of the three New York City airports for each month. We can also group by a second variable month using group_by(origin, month):

# A tibble: 36 x 3
# Groups:   origin [3]
   origin month count
   <chr>  <int> <int>
 1 EWR        1  9893
 2 EWR        2  9107
 3 EWR        3 10420
 4 EWR        4 10531
 5 EWR        5 10592
 6 EWR        6 10175
 7 EWR        7 10475
 8 EWR        8 10359
 9 EWR        9  9550
10 EWR       10 10104
# … with 26 more rows

Observe that there are 36 rows to by_origin_monthly because there are 12 months for 3 airports (EWR, JFK, and LGA).

Why do we group_by(origin, month) and not group_by(origin) and then group_by(month)? Let’s investigate:

# A tibble: 12 x 2
   month count
   <int> <int>
 1     1 27004
 2     2 24951
 3     3 28834
 4     4 28330
 5     5 28796
 6     6 28243
 7     7 29425
 8     8 29327
 9     9 27574
10    10 28889
11    11 27268
12    12 28135

What happened here is that the second group_by(month) overwrote the grouping structure meta-data of the earlier group_by(origin), so that in the end we are only grouping by month. The lesson here is if you want to group_by() two or more variables, you should include all the variables at the same time in the same group_by() adding a comma between the variable names.

Learning check

(LC3.5) Recall from Chapter 2 when we looked at temperatures by months in NYC. What does the standard deviation column in the summary_monthly_temp data frame tell us about temperatures in NYC throughout the year?

(LC3.6) What code would be required to get the mean and standard deviation temperature for each day in 2013 for NYC?

(LC3.7) Recreate by_monthly_origin, but instead of grouping via group_by(origin, month), group variables in a different order group_by(month, origin). What differs in the resulting dataset?

(LC3.8) How could we identify how many flights left each of the three airports for each carrier?

(LC3.9) How does the filter() operation differ from a group_by() followed by a summarize()?

3.5 mutate existing variables

Diagram of mutate() columns.

FIGURE 3.5: Diagram of mutate() columns.

Another common transformation of data is to create/compute new variables based on existing ones. For example, say you are more comfortable thinking of temperature in degrees Celsius (°C) instead of degrees Fahrenheit (°F). The formula to convert temperatures from °F to °C is

\[ \text{temp in C} = \frac{\text{temp in F} - 32}{1.8} \]

We can apply this formula to the temp variable using the mutate() function from the dplyr package, which takes existing variables and mutates them to create new ones.

In this code, we mutate() the weather data frame by creating a new variable temp_in_C = (temp - 32) / 1.8 and then overwrite the original weather data frame. Why did we overwrite the data frame weather, instead of assigning the result to a new data frame like weather_new? As a rough rule of thumb, as long as you are not losing original information that you might need later, it’s acceptable practice to overwrite existing data frames with updated ones, as we did here. On the other hand, why did we not overwrite the variable temp, but instead created a new variable called temp_in_C? Because if we did this, we would have erased the original information contained in temp of temperatures in Fahrenheit that may still be valuable to us.

Let’s now compute monthly average temperatures in both °F and °C using the group_by() and summarize() code we saw in Section 3.4:

# A tibble: 12 x 3
   month mean_temp_in_F mean_temp_in_C
   <int>          <dbl>          <dbl>
 1     1           35.6           2.02
 2     2           34.3           1.26
 3     3           39.9           4.38
 4     4           51.7          11.0 
 5     5           61.8          16.6 
 6     6           72.2          22.3 
 7     7           80.1          26.7 
 8     8           74.5          23.6 
 9     9           67.4          19.7 
10    10           60.1          15.6 
11    11           45.0           7.22
12    12           38.4           3.58

Let’s consider another example. Passengers are often frustrated when their flight departs late, but aren’t as annoyed if, in the end, pilots can make up some time during the flight. This is known in the airline industry as gain, and we will create this variable using the mutate() function:

Let’s take a look at only the dep_delay, arr_delay, and the resulting gain variables for the first 5 rows in our updated flights data frame in Table 3.1.

TABLE 3.1: First five rows of departure/arrival delay and gain variables
dep_delay arr_delay gain
2 11 -9
4 20 -16
2 33 -31
-1 -18 17
-6 -25 19

The flight in the first row departed 2 minutes late but arrived 11 minutes late, so its “gained time in the air” is a loss of 9 minutes, hence its gain is 2 - 11 = -9. On the other hand, the flight in the fourth row departed a minute early (dep_delay of -1) but arrived 18 minutes early (arr_delay of -18), so its “gained time in the air” is \(-1 - (-18) = -1 + 18 = 17\) minutes, hence its gain is +17.

Let’s look at some summary statistics of the gain variable by considering multiple summary functions at once in the same summarize() code:

# A tibble: 1 x 8
    min    q1 median    q3   max  mean    sd missing
  <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl>   <int>
1  -196    -3      7    17   109  5.66  18.0    9430

We see for example that the average gain is +5 minutes, while the largest is +109 minutes! However, this code would take some time to type out in practice. We’ll see later on in Subsection 5.1.1 that there is a much more succinct way to compute a variety of common summary statistics: using the skim() function from the skimr package.

Recall from Section 2.5 that since gain is a numerical variable, we can visualize its distribution using a histogram.

Histogram of gain variable.

FIGURE 3.6: Histogram of gain variable.

The resulting histogram in Figure 3.6 provides a different perspective on the gain variable than the summary statistics we computed earlier. For example, note that most values of gain are right around 0.

To close out our discussion on the mutate() function to create new variables, note that we can create multiple new variables at once in the same mutate() code. Furthermore, within the same mutate() code we can refer to new variables we just created. As an example, consider the mutate() code Hadley Wickham and Garrett Grolemund show in Chapter 5 of R for Data Science (Grolemund and Wickham 2017):

Learning check

(LC3.10) What do positive values of the gain variable in flights correspond to? What about negative values? And what about a zero value?

(LC3.11) Could we create the dep_delay and arr_delay columns by simply subtracting dep_time from sched_dep_time and similarly for arrivals? Try the code out and explain any differences between the result and what actually appears in flights.

(LC3.12) What can we say about the distribution of gain? Describe it in a few sentences using the plot and the gain_summary data frame values.

3.6 arrange and sort rows

One of the most commonly performed data wrangling tasks is to sort a data frame’s rows in the alphanumeric order of one of the variables. The dplyr package’s arrange() function allows us to sort/reorder a data frame’s rows according to the values of the specified variable.

Suppose we are interested in determining the most frequent destination airports for all domestic flights departing from New York City in 2013:

# A tibble: 105 x 2
   dest  num_flights
   <chr>       <int>
 1 ABQ           254
 2 ACK           265
 3 ALB           439
 4 ANC             8
 5 ATL         17215
 6 AUS          2439
 7 AVL           275
 8 BDL           443
 9 BGR           375
10 BHM           297
# … with 95 more rows

Observe that by default the rows of the resulting freq_dest data frame are sorted in alphabetical order of destination. Say instead we would like to see the same data, but sorted from the most to the least number of flights (num_flights) instead:

# A tibble: 105 x 2
   dest  num_flights
   <chr>       <int>
 1 LEX             1
 2 LGA             1
 3 ANC             8
 4 SBN            10
 5 HDN            15
 6 MTJ            15
 7 EYW            17
 8 PSP            19
 9 JAC            25
10 BZN            36
# … with 95 more rows

This is, however, the opposite of what we want. The rows are sorted with the least frequent destination airports displayed first. This is because arrange() always returns rows sorted in ascending order by default. To switch the ordering to be in “descending” order instead, we use the desc() function as so:

# A tibble: 105 x 2
   dest  num_flights
   <chr>       <int>
 1 ORD         17283
 2 ATL         17215
 3 LAX         16174
 4 BOS         15508
 5 MCO         14082
 6 CLT         14064
 7 SFO         13331
 8 FLL         12055
 9 MIA         11728
10 DCA          9705
# … with 95 more rows

3.7 join data frames

Another common data transformation task is “joining” or “merging” two different datasets. For example, in the flights data frame, the variable carrier lists the carrier code for the different flights. While the corresponding airline names for "UA" and "AA" might be somewhat easy to guess (United and American Airlines), what airlines have codes "VX", "HA", and "B6"? This information is provided in a separate data frame airlines.

We see that in airports, carrier is the carrier code, while name is the full name of the airline company. Using this table, we can see that "VX", "HA", and "B6" correspond to Virgin America, Hawaiian Airlines, and JetBlue, respectively. However, wouldn’t it be nice to have all this information in a single data frame instead of two separate data frames? We can do this by “joining” the flights and airlines data frames.

Note that the values in the variable carrier in the flights data frame match the values in the variable carrier in the airlines data frame. In this case, we can use the variable carrier as a key variable to match the rows of the two data frames. Key variables are almost always identification variables that uniquely identify the observational units as we saw in Subsection 1.4.4. This ensures that rows in both data frames are appropriately matched during the join. Hadley and Garrett (Grolemund and Wickham 2017) created the diagram shown in Figure 3.7 to help us understand how the different data frames in the nycflights13 package are linked by various key variables:

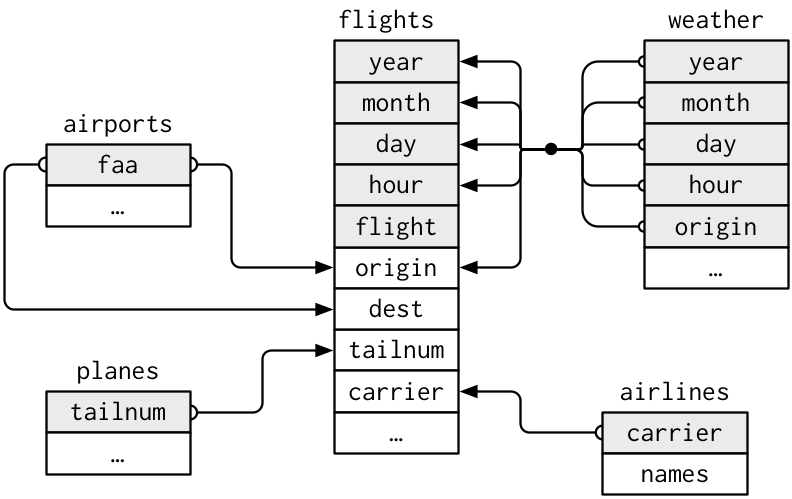
Data relationships in nycflights13 from R for Data Science.

FIGURE 3.7: Data relationships in nycflights13 from R for Data Science.

3.7.1 Matching “key” variable names

In both the flights and airlines data frames, the key variable we want to join/merge/match the rows by has the same name: carrier. Let’s use the inner_join() function to join the two data frames, where the rows will be matched by the variable carrier, and then compare the resulting data frames:

Observe that the flights and flights_joined data frames are identical except that flights_joined has an additional variable name. The values of name correspond to the airline companies’ names as indicated in the airlines data frame.

A visual representation of the inner_join() is shown in Figure 3.8 (Grolemund and Wickham 2017). There are other types of joins available (such as left_join(), right_join(), outer_join(), and anti_join()), but the inner_join() will solve nearly all of the problems you’ll encounter in this book.

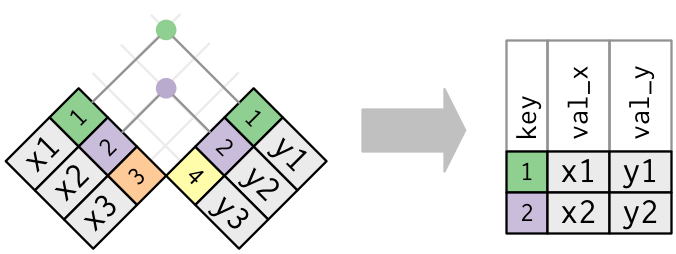
Diagram of inner join from R for Data Science.

FIGURE 3.8: Diagram of inner join from R for Data Science.

3.7.2 Different “key” variable names

Say instead you are interested in the destinations of all domestic flights departing NYC in 2013, and you ask yourself questions like: “What cities are these airports in?”, or “Is "ORD" Orlando?”, or “Where is "FLL"?”.

The airports data frame contains the airport codes for each airport:

However, if you look at both the airports and flights data frames, you’ll find that the airport codes are in variables that have different names. In airports the airport code is in faa, whereas in flights the airport codes are in origin and dest. This fact is further highlighted in the visual representation of the relationships between these data frames in Figure 3.7.

In order to join these two data frames by airport code, our inner_join() operation will use the by = c("dest" = "faa") argument with modified code syntax allowing us to join two data frames where the key variable has a different name:

Let’s construct the chain of pipe operators %>% that computes the number of flights from NYC to each destination, but also includes information about each destination airport:

# A tibble: 101 x 9
   dest  num_flights airport_name          lat    lon   alt    tz dst   tzone   
   <chr>       <int> <chr>               <dbl>  <dbl> <dbl> <dbl> <chr> <chr>   
 1 ORD         17283 Chicago Ohare Intl   42.0  -87.9   668    -6 A     America…
 2 ATL         17215 Hartsfield Jackson…  33.6  -84.4  1026    -5 A     America…
 3 LAX         16174 Los Angeles Intl     33.9 -118.    126    -8 A     America…
 4 BOS         15508 General Edward Law…  42.4  -71.0    19    -5 A     America…
 5 MCO         14082 Orlando Intl         28.4  -81.3    96    -5 A     America…
 6 CLT         14064 Charlotte Douglas …  35.2  -80.9   748    -5 A     America…
 7 SFO         13331 San Francisco Intl   37.6 -122.     13    -8 A     America…
 8 FLL         12055 Fort Lauderdale Ho…  26.1  -80.2     9    -5 A     America…
 9 MIA         11728 Miami Intl           25.8  -80.3     8    -5 A     America…
10 DCA          9705 Ronald Reagan Wash…  38.9  -77.0    15    -5 A     America…
# … with 91 more rows

In case you didn’t know, "ORD" is the airport code of Chicago O’Hare airport and "FLL" is the main airport in Fort Lauderdale, Florida, which can be seen in the airport_name variable.

3.7.3 Multiple “key” variables

Say instead we want to join two data frames by multiple key variables. For example, in Figure 3.7, we see that in order to join the flights and weather data frames, we need more than one key variable: year, month, day, hour, and origin. This is because the combination of these 5 variables act to uniquely identify each observational unit in the weather data frame: hourly weather recordings at each of the 3 NYC airports.

We achieve this by specifying a vector of key variables to join by using the c() function. Recall from Subsection 1.2.1 that c() is short for “combine” or “concatenate.”

Learning check

(LC3.13) Looking at Figure 3.7, when joining flights and weather (or, in other words, matching the hourly weather values with each flight), why do we need to join by all of year, month, day, hour, and origin, and not just hour?

(LC3.14) What surprises you about the top 10 destinations from NYC in 2013?

3.7.4 Normal forms

The data frames included in the nycflights13 package are in a form that minimizes redundancy of data. For example, the flights data frame only saves the carrier code of the airline company; it does not include the actual name of the airline. For example, the first row of flights has carrier equal to UA, but it does not include the airline name of “United Air Lines Inc.”

The names of the airline companies are included in the name variable of the airlines data frame. In order to have the airline company name included in flights, we could join these two data frames as follows:

We are capable of performing this join because each of the data frames have keys in common to relate one to another: the carrier variable in both the flights and airlines data frames. The key variable(s) that we base our joins on are often identification variables as we mentioned previously.

This is an important property of what’s known as normal forms of data. The process of decomposing data frames into less redundant tables without losing information is called normalization. More information is available on Wikipedia.

Both dplyr and SQL we mentioned in the introduction of this chapter use such normal forms. Given that they share such commonalities, once you learn either of these two tools, you can learn the other very easily.

Learning check

(LC3.15) What are some advantages of data in normal forms? What are some disadvantages?

3.8 Other verbs

Here are some other useful data wrangling verbs:

  • select() only a subset of variables/columns.
  • rename() variables/columns to have new names.
  • Return only the top_n() values of a variable.

3.8.1 select variables

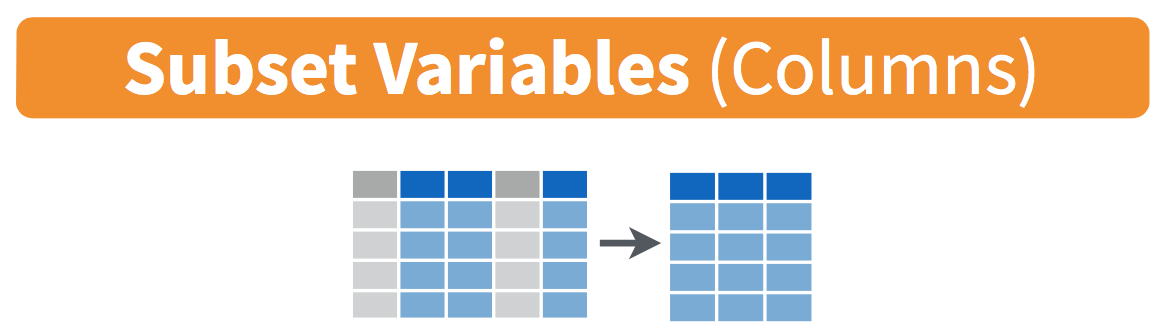
Diagram of select() columns.

FIGURE 3.9: Diagram of select() columns.

We’ve seen that the flights data frame in the nycflights13 package contains 19 different variables. You can identify the names of these 19 variables by running the glimpse() function from the dplyr package:

However, say you only need two of these 19 variables, say carrier and flight. You can select() these two variables:

This function makes it easier to explore large datasets since it allows us to limit the scope to only those variables we care most about. For example, if we select() only a smaller number of variables as is shown in Figure 3.9, it will make viewing the dataset in RStudio’s spreadsheet viewer more digestible.

Let’s say instead you want to drop, or de-select, certain variables. For example, consider the variable year in the flights data frame. This variable isn’t quite a “variable” because it is always 2013 and hence doesn’t change. Say you want to remove this variable from the data frame. We can deselect year by using the - sign:

Another way of selecting columns/variables is by specifying a range of columns:

This will select() all columns between month and day, as well as between arr_time and sched_arr_time, and drop the rest.

The select() function can also be used to reorder columns when used with the everything() helper function. For example, suppose we want the hour, minute, and time_hour variables to appear immediately after the year, month, and day variables, while not discarding the rest of the variables. In the following code, everything() will pick up all remaining variables:

Lastly, the helper functions starts_with(), ends_with(), and contains() can be used to select variables/columns that match those conditions. As examples,

3.8.2 rename variables

Another useful function is rename(), which as you may have guessed changes the name of variables. Suppose we want to only focus on dep_time and arr_time and change dep_time and arr_time to be departure_time and arrival_time instead in the flights_time data frame:

Note that in this case we used a single = sign within the rename(). For example, departure_time = dep_time renames the dep_time variable to have the new name departure_time. This is because we are not testing for equality like we would using ==. Instead we want to assign a new variable departure_time to have the same values as dep_time and then delete the variable dep_time. Note that new dplyr users often forget that the new variable name comes before the equal sign.

3.8.3 top_n values of a variable

We can also return the top n values of a variable using the top_n() function. For example, we can return a data frame of the top 10 destination airports using the example from Subsection 3.7.2. Observe that we set the number of values to return to n = 10 and wt = num_flights to indicate that we want the rows corresponding to the top 10 values of num_flights. See the help file for top_n() by running ?top_n for more information.

Let’s further arrange() these results in descending order of num_flights:

Learning check

(LC3.16) What are some ways to select all three of the dest, air_time, and distance variables from flights? Give the code showing how to do this in at least three different ways.

(LC3.17) How could one use starts_with(), ends_with(), and contains() to select columns from the flights data frame? Provide three different examples in total: one for starts_with(), one for ends_with(), and one for contains().

(LC3.18) Why might we want to use the select function on a data frame?

(LC3.19) Create a new data frame that shows the top 5 airports with the largest arrival delays from NYC in 2013.

3.9 Conclusion

3.9.1 Summary table

Let’s recap our data wrangling verbs in Table 3.2. Using these verbs and the pipe %>% operator from Section 3.1, you’ll be able to write easily legible code to perform almost all the data wrangling and data transformation necessary for the rest of this book.

TABLE 3.2: Summary of data wrangling verbs
Verb Data wrangling operation
filter() Pick out a subset of rows
summarize() Summarize many values to one using a summary statistic function like mean(), median(), etc.
group_by() Add grouping structure to rows in data frame. Note this does not change values in data frame, rather only the meta-data
mutate() Create new variables by mutating existing ones
arrange() Arrange rows of a data variable in ascending (default) or descending order
inner_join() Join/merge two data frames, matching rows by a key variable

Learning check

(LC3.20) Let’s now put your newly acquired data wrangling skills to the test!

An airline industry measure of a passenger airline’s capacity is the available seat miles, which is equal to the number of seats available multiplied by the number of miles or kilometers flown summed over all flights.

For example, let’s consider the scenario in Figure 3.10. Since the airplane has 4 seats and it travels 200 miles, the available seat miles are \(4 \times 200 = 800\).

Example of available seat miles for one flight.

FIGURE 3.10: Example of available seat miles for one flight.

Extending this idea, let’s say an airline had 2 flights using a plane with 10 seats that flew 500 miles and 3 flights using a plane with 20 seats that flew 1000 miles, the available seat miles would be \(2 \times 10 \times 500 + 3 \times 20 \times 1000 = 70,000\) seat miles.

Using the datasets included in the nycflights13 package, compute the available seat miles for each airline sorted in descending order. After completing all the necessary data wrangling steps, the resulting data frame should have 16 rows (one for each airline) and 2 columns (airline name and available seat miles). Here are some hints:

  1. Crucial: Unless you are very confident in what you are doing, it is worthwhile not starting to code right away. Rather, first sketch out on paper all the necessary data wrangling steps not using exact code, but rather high-level pseudocode that is informal yet detailed enough to articulate what you are doing. This way you won’t confuse what you are trying to do (the algorithm) with how you are going to do it (writing dplyr code).
  2. Take a close look at all the datasets using the View() function: flights, weather, planes, airports, and airlines to identify which variables are necessary to compute available seat miles.
  3. Figure 3.7 showing how the various datasets can be joined will also be useful.
  4. Consider the data wrangling verbs in Table 3.2 as your toolbox!

3.9.2 Additional resources

An R script file of all R code used in this chapter is available here.

If you want to further unlock the power of the dplyr package for data wrangling, we suggest that you check out RStudio’s “Data Transformation with dplyr” cheatsheet. This cheatsheet summarizes much more than what we’ve discussed in this chapter, in particular more intermediate level and advanced data wrangling functions, while providing quick and easy-to-read visual descriptions. In fact, many of the diagrams illustrating data wrangling operations in this chapter, such as Figure 3.1 on filter(), originate from this cheatsheet.

In the current version of RStudio in late 2019, you can access this cheatsheet by going to the RStudio Menu Bar -> Help -> Cheatsheets -> “Data Transformation with dplyr.” You can see a preview in the figure below.

Data Transformation with dplyr cheatsheet.

FIGURE 3.11: Data Transformation with dplyr cheatsheet.

On top of the data wrangling verbs and examples we presented in this section, if you’d like to see more examples of using the dplyr package for data wrangling, check out Chapter 5 of R for Data Science (Grolemund and Wickham 2017).

3.9.3 What’s to come?

So far in this book, we’ve explored, visualized, and wrangled data saved in data frames. These data frames were saved in a spreadsheet-like format: in a rectangular shape with a certain number of rows corresponding to observations and a certain number of columns corresponding to variables describing these observations.

We’ll see in the upcoming Chapter 4 that there are actually two ways to represent data in spreadsheet-type rectangular format: (1) “wide” format and (2) “tall/narrow” format. The tall/narrow format is also known as “tidy” format in R user circles. While the distinction between “tidy” and non-“tidy” formatted data is subtle, it has immense implications for our data science work. This is because almost all the packages used in this book, including the ggplot2 package for data visualization and the dplyr package for data wrangling, all assume that all data frames are in “tidy” format.

Furthermore, up until now we’ve only explored, visualized, and wrangled data saved within R packages. But what if you want to analyze data that you have saved in a Microsoft Excel, a Google Sheets, or a “Comma-Separated Values” (CSV) file? In Section 4.1, we’ll show you how to import this data into R using the readr package.

References

Grolemund, Garrett, and Hadley Wickham. 2017. R for Data Science. First. Sebastopol, CA: O’Reilly Media. https://r4ds.had.co.nz/.